Songyuli's blog
0%

z变换

Posted on Edited on Disqus:

z变换

离散时间傅里叶变换的局限性与z变换介绍

傅里叶变换对于一部分序列并不收敛
例如$X(\omega)=\sum x(n)e^{-j\omega n}$我们需要其收敛,需要判断其条件

可以使用三角不等式,最终会得到前者收敛的条件为$\sum |x(n)|<\infty$(绝对可和)

我们之前所讨论的稳定性,可以得到一个稳定系统中的$H(\omega)$是绝对可和的

一个例子

对于$x(n)=2^nu(n)$,我们能够注意到$\sum x(n)=\infty$,因此傅里叶变换不收敛

根据一个非常常用的结论,假如我们有一个(模)指数下降的序列,那么其傅里叶变换必然收敛
因此我们可以采用类似于处理拉普拉斯变换的方法,乘以一个指数下降的数列

如果我们选取一个$r>2$,那么我们能够得到一个收敛的序列$x(n)r^{-n}$

z变换定义

$$X(z)=\sum x(n)z^{-n}$$
与傅里叶变换的联系之处在于
$$X(\omega)=X(z)|_{z=e^{j\omega}}$$

对于某些$r$值,z变换会收敛,对于某些$r$值,其并不会收敛

如何处理

这里视频中有许多,但我认为只需要将整个模长保持在小于1的部分,那么我们就可以绘制出一个收敛圆
特别地,如果收敛圆包含了单位圆,那么我们可以知道这个序列的离散傅里叶变换也是收敛的

同时,我们也要注意到,对于不同的$u(n)$情况,会有不同的收敛域

在这里讨论的极点是使用求和公式求出来的结果,而对于不同的条件下,其可能是零点,也有可能是极点

Alt text

收敛域的一些性质

  1. 收敛的范围总是被限制在极点和(0/$\infty$)
  2. 对于有限长的序列,收敛域为$0<|z|<\infty$
  3. 右侧序列($n$有下界),那么$|z|$有下界
  4. 左侧序列($n$有上界),那么$|z|$有上界
  5. 两侧序列($n$无界),那么有$R_{x-}<|z|<R_{x+}$

下面展示了一个判断傅里叶变换是否存在的例子

Alt text

而对于两侧序列的判定,我们可以参考
$$(\frac{1}{2})^{|n|}$$
其可以被视作两侧序列,而$|z|$的收敛范围是$(\frac{1}{2},2)$

z变换的性质

我们仍然可以得到一些像卷积定理的内容
$$y(n)=x(n)*h(n)$$
$$Y(z)=X(z)H(z)$$

我们也可以通过$z$变换的过程得到信号序列的一些性质

  1. 如果信号序列是稳定的,那么单位圆必然在收敛域中
  2. 如果信号序列是关联的,那么必然是一个右侧序列

使用线性差分方程表示的例子

$$y(n)-\frac{1}{2}y(n-1)=x(n)$$
我们需要使用一些好用的性质
$$y(n)\lrArr Y(z)$$
$$y(n+n_0)\lrArr z^{n_0}Y(z)$$
我们可以得到一个代数方程,得到
$$H(z)=\frac{1}{1-\frac{1}{2}z^{-1}}$$

这里和那拉普拉斯变换解微分方程如出一辙

同时我们需要注意到,这里的收敛域会随着序列中$n$条件的变化而变化(如图所示)
Alt text

z反变换

$$X(z)=\sum x(n)z^{-n}$$
z反变换可以从$X(z)$得到$x(n)$

直接观察法

例如
$$a^nu(n)\lrArr \frac{1}{1-az^{-1}}$$
这样的序列,我们可以直接从z反变换的结果反推出原本的过程

注意,这里需要讨论$|z|$的范围(改变$n$的范围)

暴力展开

例如对于$X(z)=\frac{1}{1-az^{-1}}$的反变换,我们可以有这个式子的展开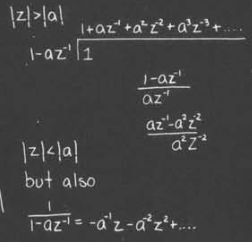
Alt text

我们可以看到,这里对应于$n>0$或者$n<0$的情况,两者有着不同的展开
但是这种方法我们只能得到一系列的式子,我们还要将其综合起来

部分分式展开

考虑一个一般有理函数
$$F(x)=\frac{P(x)}{Q(x)}=\sum\frac{R_k}{x-x_k}$$
其中$x_k$为$Q$的零点,而$R_k$为留数

为了讨论方便,我们假定分母次数更高,并且没有重根
这里使用了一些留数定理的内容

可以使用两种不同的方法(视作$z$和$z^{-1}$)
下面展示了一个例子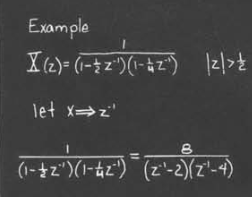
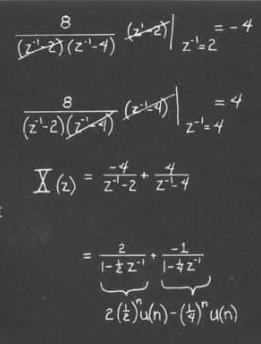
Alt text
Alt text

但是这种方法只适用于分式的情况,因此不能广泛地使用(但是在讨论一些性质的时候非常有用)

路径积分法

我们直接给出结论
$$x(n)=\frac{1}{2\pi j}\int_C X(z)z^{n-1}dz$$
($C$环路为包含原点的边缘在收敛域内的环路)

这个公式的证明实际上来自于$n$阶导的柯西公式

在实际计算的时候需要使用留数定理计算($X(z)z^{n-1}$)的留数

一个简单的例子

我们以$X(z)=\frac{1}{1-\frac{1}{2}z^{-1}}$
其具体的做法如下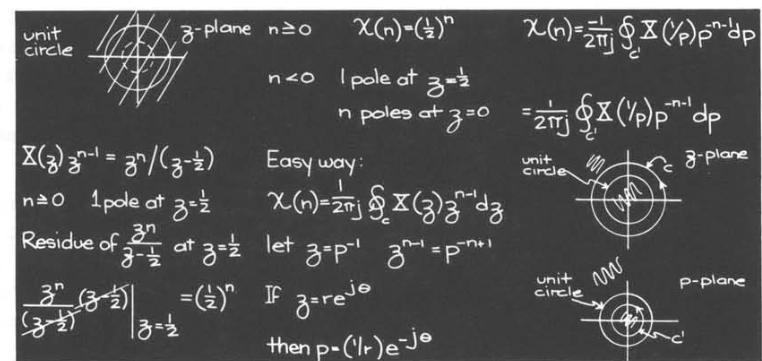
Alt text

可以看出来,对于$n>0$的情况,计算要显得方便的很多,但是$n<0$的话,可以考虑使用变量代换的方式计算
不过我觉得直接继续用留数定理的公式还是方便的

一些结论以及重要的注意事项

  1. 我们讨论的时候强调上面的次数要小于下面的次数,这里体现出关联性(否则就会有$z$的正数次项留出来)
  2. 对于前面讨论的着一种情况,我们需要小心在环路积分之余,可能会有单独留出来的项
  3. 展开的时候经常会犯迷糊,记得把式子展开为$a_nz^{-n}$的形式,其中注意$z$的符号

z变换的相关性质

频率响应的几何意义

卷积性质

对于$y(n)=x(n)*h(z)$,我们可以得到z变换$X(z)H(z)=Y(z)$

同时,我们也可以得到,在单位圆上的z变换就是傅里叶变换

作为一个例子,我们请出我们的老朋友$H(z)=\frac{z}{z-a}$,
进一步,可以把$z$看作矢量,这样就可以看作是从零点出来的矢量除以从极点出来的矢量
相应的,模长就是两者相除,辐角就是两者相减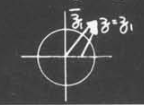
Alt text
Alt text

接下来,我们考虑$z$是在单位圆上的矢量,那么$z$的模长不再改变

在整个$z$旋转的时候,$z-a$的模长先增加后减小
这样我们就可以简单地得到频率响应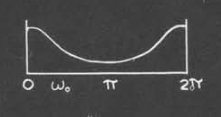
Alt text

一般讨论

对于频率响应$|H(e^{j\omega})|=\frac{\Pi length zero}{\Pi length pole}$,
对于相位相应,则有
Alt text

这意味着我们可以仅仅知道所有的极点和零点,就可以大致知道频率响应和相位谱
如果有多重极点的情况,可以当成多个极点计算

变换性质

一般变换性质(可以和连续状况类比)

下面列举出了最为有用的一些性质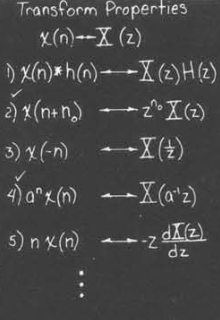
Alt text

变换性质与几何性质

以第四个性质为例,我们可以考虑极点与零点,会得到原本的$z-z_0$变成了$a^{-1}(z-az_0)$

如果$a$是实数,那么极点(零点)会在轴上移动,如果是复数,那么就同时会改变角度

性质在Boxcar序列中的应用

Boxcar序列

$$x(n)=1 (0\le n\le (N-1)$$
Alt text
我们可以将Boxcar序列视作为两个阶梯序列相减$x(n)=u(n)-u(n-N)$

Boxcar的z变换

使用上面的观点,可以得到
$$X(z)=\frac{1}{1-z^{-1}}-\frac{z^{-N}}{1-z^{-1}}=\frac{z^N-1}{z^{N-1}(z-1)}$$

接下来,我们可以注意到整个系统在单位圆上有一个极点,在原点有$N-1$个零点
而对于零点,则是相当于在单位圆上均匀分布的点

这里需要注意到,一个零点和一个极点约掉了
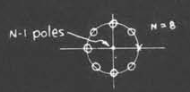
Alt text

Boxcar的频率相应

分母上不构成影响,所以只需要讨论零点伸出来的矢量的影响(越靠近那个确实的零点,整体的模长值越大)
Alt text

或者直接使用计算法,可以得到
$$X(\omega)=\frac{1-e^{-j\omega N}}{1-e^{-j\omega}}$$
通过化简,可以得到
$$e^{j\omega\frac{N-1}{2}}\frac{\omega \frac{N}{2}}{\frac{N}{2}}$$

而我们展示其图象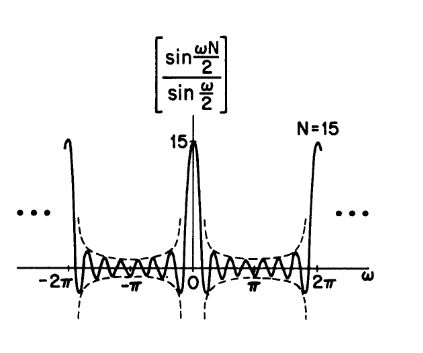
Alt text

可以看出,我们的估计还算是相当不错的