数字信号处理介绍

数字信号处理具有非常强的扩展性,例如对于频率响应不一致的器件进行补偿
而对于一些图象处理领域,可以将图像看作为二维信号.

离散时间系统

以一个数字滤波器为例包含以下部分:

采样器
连续/数字信号转换器(C/D)
数字滤波
数字/连续信号转换器(D/C)
滤波器

C/D信号转换器的效果

存在有倍频变形,一般可以使用低通滤波器实现,然而,如果信号频谱本来就沿伸的比较大,那么就会出现混叠的情况
因此数字信号处理时需要小心地处理高频情况
因此,数字信号采样率必须远大于关心的信号的频率的两倍

相似地,对于数字信号处理的情况,整个数字信号处理的波形会发生变化

而在数字滤波器中,其形状与模拟滤波器相同,但是具有不同的频率坐标轴

对于数字滤波器可能会发现在采样频率的倍频发生周期行为

似乎一定的采样频率可以等效于一个低通滤波器,但是我不清楚怎么搞的

离散时间信号与系统

对于我们所关心的离散时间系统,我们主要讨论的是有一列一定长度$n$的信号

一些常用的离散时间信号序列

单位

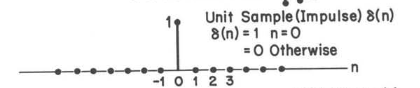
单位阶跃

两者之间联系

实际上单位样本$\delta(n)$可以直接从单位阶跃样本中直接得到
$$\delta(n)=u(n)-u(n-1)$$

相似地,也可以用求和来实现逆操作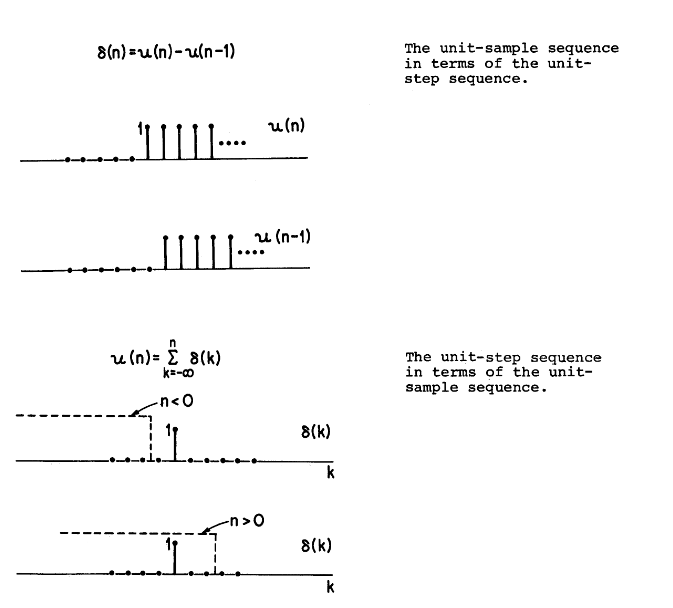

其他的一些常见样本

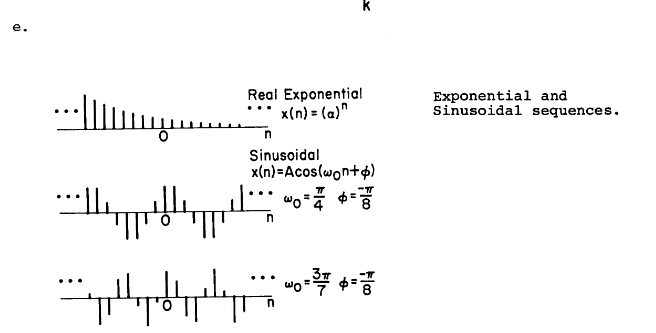
需要注意到,一些原本是周期的信号在数字信号采样下不一定是周期信号

这些信号可以用来描述更加普遍的信号(相当于函数展开)

将一般信号使用特殊信号的转化

使用单位脉冲转化

(这个应该算是相当简单和显然的)

离散时间系统的性质

线性性
具有时间平移对称性$x(n-n_0)->y(n-n_0)$

一般表达(卷积和)

对于$x(n)=\sum x(k)\delta (n-k)$在经过一个系统后,我们可以得到其相应$y(n)=\sum y(k)\rho (n-k)$,其中$rho$为脉冲响应

这可以用卷积的方式来理解这个性质(我们可以把$x$和$\delta$地位互换)

卷积和的计算

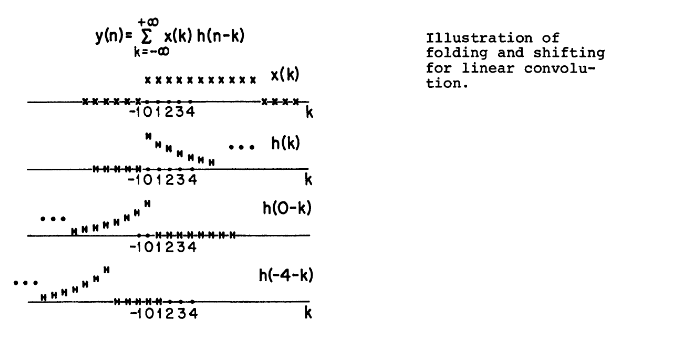
卷积和来源于线性性和时间平移不变性

稳定性与相关性

稳定性

如果系统的输入是有界的,那么系统的输出是有界

例如我们可以判断一组基是不是有界的$(\frac{1}{2})^nh(n)$就是有界的,但很显然$2^nh(n)$不是

判断一个系统的稳定性有一个充要条件:单位冲激响应$h(n)$是绝对可和的

线性常系数差分方程

输入$x(n)$和输出$y(n)$满足$n$阶线性常系数差分方程可以被表示为
$$\sum_{k=0}^{N}a_ky(n-k)=\sum_{r=0}^Mb_rx(n-r)$$

一些特殊情况

对于零阶方程,$b_r$系数的确定可以看作是脉冲响应

而对于非零阶的方程,那么我们可以将方程写作如下形式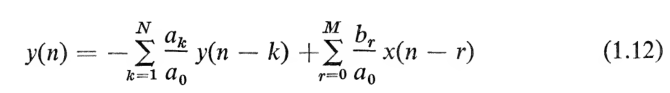

那么我们可以利用输入和过去的输出实现对于当前输出的预测(这个时候需要边界条件)

例如,下面一个一阶差分方程展示出一个如何求脉冲响应的例子

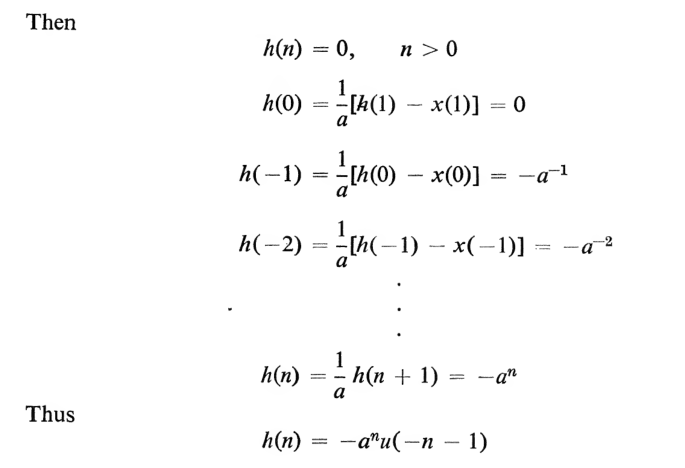
需要根据边界条件合理地选择差分方程方向

注意,不是每个差分方程(包含边界条件)都对应线性和时间平移不变的系统(似乎一般需要满足边界条件齐次)

系统的频率响应

复指数的特点

复指数函数是特性函数,也就是说,如果输入是一个复指数,那么输出是输入乘上一个系数的结果(其中实数部分表示振幅,复数部分表示相位)

因此,对于输入为$x(n)=e^{j\omega n}$,我们可以有输出
$$y(n)=H(e^{j\omega n})e$$

相似地,我们可以将任意一个正弦或余弦函数转化成复指数运算

如果使用上一部分的差分方程的例子研究频率响应,我们可以得到一个幅频响应呈现周期变化的系统

频率响应的重要性质

频率响应的自变量是连续的
频率响应是$\omega$的周期函数,周期为$2\pi$(注意,这里的自变量是$n$)

离散时间系统的傅里叶变换

之前我们讨论过系统的频率响应,我们知道对于一个复指数的输入,输出也可以被表示为复指数.我们现在要研究如何从频率响应得到冲激响应
如果我们分析$H(e^{j\omega})$的性质,我们会发现其作为一个周期函数,可以有傅里叶级数展开,由于其周期为$2\pi$,我们可以得到
$$H(\omega)=\sum_{n=-\infin}^{\infin}h(n)e^{-\omega n}$$
通过比较,我们可以发现此时的$h(n)$就是系统冲激响应,因此我们可以得到一个结论:
系统的冲激响应和频率响应构成傅里叶变换对

任意信号的傅里叶变换

$$X(\omega)=\sum_{n=-\infin}^{n=\infin}x(n)e^{-j\omega n}$$
$$x(n)=\frac{1}{2\pi}\int_{-\pi}^{\pi}X(\omega)e^{j\omega n}d\omega$$

这里和一般的傅里叶级数的关系可以看作是”反过来”的,离散的是时域,连续且周期变化的是频域

卷积特性

$$x(n)*y(n)\lrArr X(\omega)Y(\omega)$$
这个似乎和连续的卷积相似

一种更具有启发性的观点

对于一个系统,我们有频域转换$e^{j\omega n}\rArr H(\omega)e^{j\omega n}$

那么我们可以有
$$\int X(\omega)e^{j\omega n}\rArr \int A(\omega)H(e^{j\omega})e^{j\omega n}d\omega$$

等式左边是输入信号$x(n)$,等式右边则为输出信号$y(n)$

对于某一特定的频率信号,我们是乘积关系
对于冲激响应,我们是卷积关系
两者可以使用傅里叶变换联合在一起

对偶性

对于$x(n)$为实信号的情况,我们可以得到$X(\omega)=X^*(-\omega)$

进一步,我们可以将$X$分解为实部与虚部$X=X_R+jX_I$
那么我们可以有对于实信号,有
$$X_R(\omega)=X_R(-\omega),X_I(\omega)=X_R(-\omega)$$
实部为偶函数,虚部为奇函数,相似的,对于傅里叶变换的模关于$\omega$为偶函数,辐角为奇函数

与连续时间傅里叶变换的关系

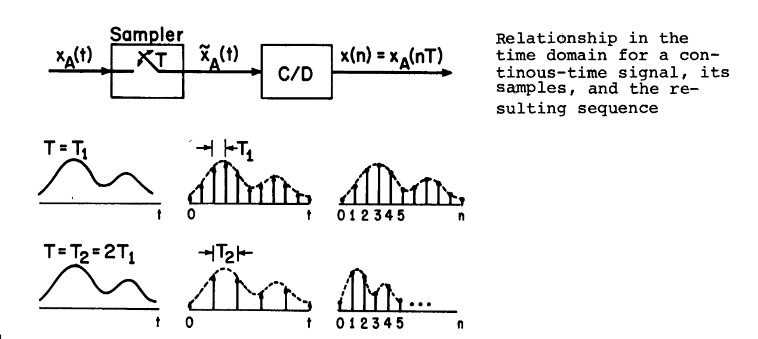
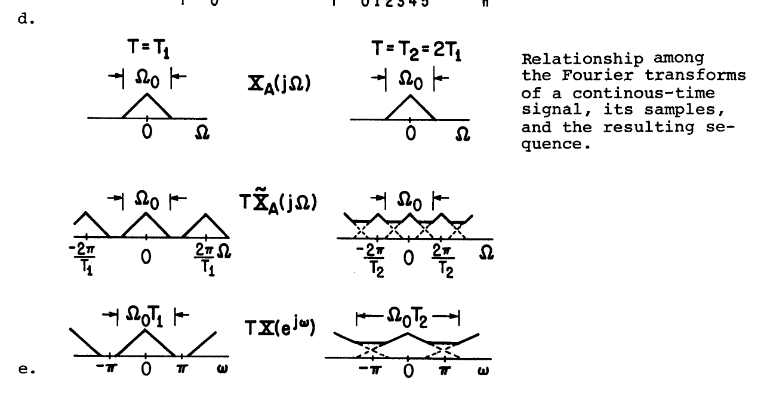
将时间$t$转换为$n$,我们可以得到对应于离散时间变量$n$,其所对应的$t$为$nT$,其中$T$为两个采样点之间的距离,图上展示了不同采样间隔下的波形的形状

我们可以考虑具有傅里叶变换的模拟信号
$$x_\alpha (t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X_\alpha(j\Omega)e^{j\Omega t}d\Omega$$

这里为了和离散时间的傅里叶变换相契合,我们把变换和反变换颠倒了一下

从连续到冲激的转换

我们可以将转换看作为冲激的叠加

$$x’A=\sum{-\infty}^{\infty} x_A(nT)\delta(t-nT)$$

这里的做法比较类似于将卷积得到的结果和直接傅里叶变换得到的结果之间进行比较

这里最左边部分需要使用到泊松求和方程
$$\sum_{n=-\infty}^{\infty}f(n)=\sum_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x)e^{-2\pi jkx}$$

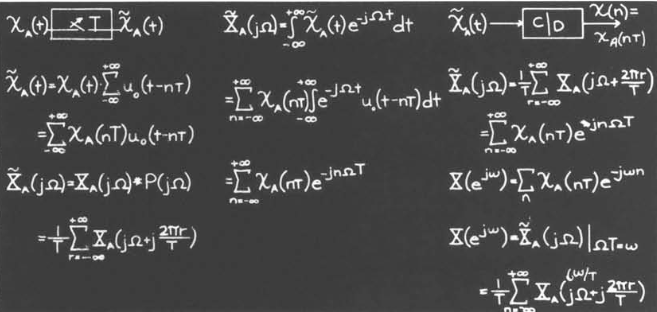
注意最后一个式子,这里可以得到离散傅里叶变换的频率谱与连续傅里叶变换谱的关系,并且包含了由于采样所带来的周期性(采样定理)

实际应用时的注意事项

考虑一个数字滤波器的效果时,需要将一个模拟输入(频率轴下)进行抽样,然后经过数字滤波器的效果,最后再恢复(低通滤波)
在一些非关联的系统(许多非实时系统)中,可以构造数字滤波器使得原有滤波器不再产生相位变化

Songyuli's blog

数字信号处理(介绍至离散时间傅里叶变换)