IIR系统的设计
在之前我们讨论了数字滤波器的表示等,而在这一部分,我们将讨论如何设计一个数字滤波器
对于一个滤波器而言,一个频率的波输入后,只会改变振幅与相位,因此我们可以将不同频率带的信号滤除
相似的,我们可以认为数字滤波器的设计就是设计一个具有我们想要的频率响应
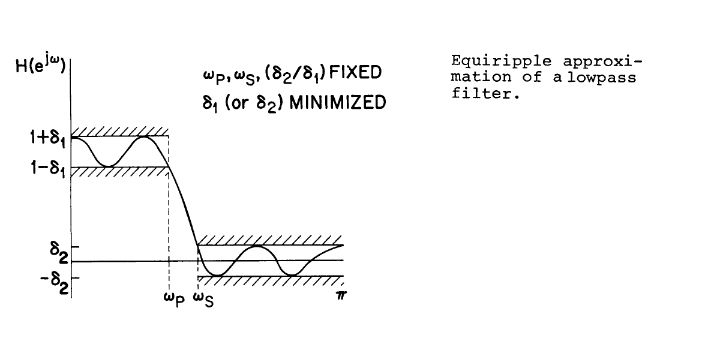
以低通滤波器为例
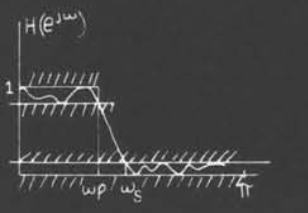
设计的技术
我们要做的是将一个理想的滤波器粗略化为一个可以实现的滤波器(允许一些变化)
之后主要设计出来的是一个关于z的有理函数
- 在模拟的情况下分析
- 从连续时间到分离时间(注意我们不是尝试让数字滤波器接近模拟滤波器)
- 计算方法
将模拟滤波器技术转移到数字滤波器的要求
我们将连续状态下的直接映射到数字滤波器的情况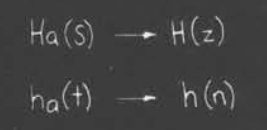
同时,如果设计的模拟滤波器是稳定的,那么相对应的数字滤波器也是稳定的
将微分变为差分
对于模拟滤波器而言,有微分方程
$$\sum_{k=0}^N c_k\frac{d^k y_a(t)}{dt^k}=\sum_{k=0}^Md_k\frac{d^k x_a(t)}{dt^k}$$
直接让$\frac{dy_a}{dt}->\Delta^{(1)} [y(n)]$
同时也可以表示高阶差分$\Delta^{(n)}=\Delta^{(1)}[\Delta^{(k-1)}y(n)]$
如何理解拉普拉斯变换与z变换
拉普拉斯变换下
$$\frac{dy_a(t)}{dt}=sY_a(s)$$
z变换下
$$\frac{y(n+1)-y(n)}{T}=\frac{z-1}{T}Y(z)$$
因此我们可以得到一个映射
$$H(z)=Ha(s)|_{s=\frac{z-1}{T}}$$
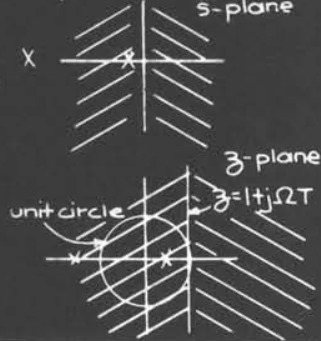
可以注意到$s$平面上的轴(即为拉普拉斯变换等于傅里叶变换)映射到$z$平面成为了一条直线,不再是单位圆,所以两个模型的频率响应并不对应
同时,这也不能保证数字滤波器收敛
实际上,如果我们的采样率足够高,那么在$z$平面上频率响应接近切线,表明使用差分代替微分在渐近情况下是合理的
脉冲不变量法
我们也可以通过选择与模拟信号输入相同(按照采样率缩放)的脉冲响应
有$h(n)=h_a(nT)$
那么系统的DFT就是
$$H(e^{j\omega})=\frac{1}{T}\sum H_a[\frac{j\omega}{T}+\frac{j2\pi k}{T}]$$
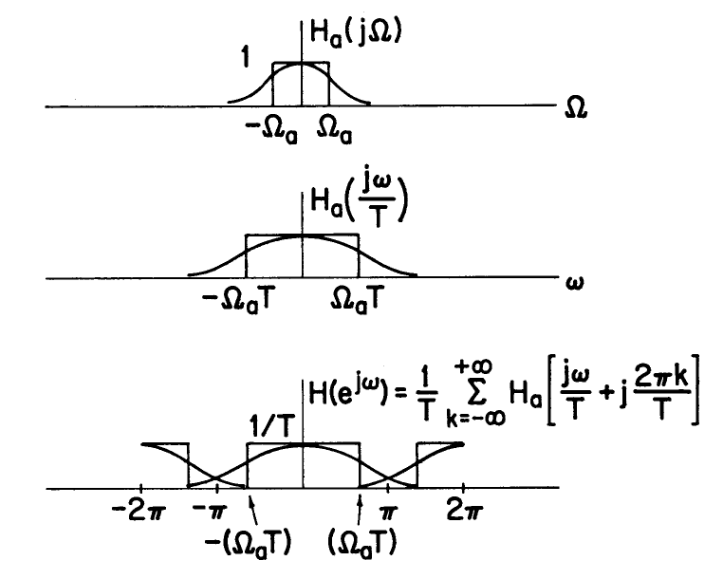
实际使用的时候会存在混叠的问题(在接近采样频率的时候会出现问题)
同时我们也要注意到,脉冲不变不代表阶跃不变
同时,我们也可以使用极点的角度看待这个问题
在连续信号中,有极点
$$H_a(s)=\sum\frac{A_k}{s-s_k}$$
将其转换到数字($z$平面)
$$H(z)=\sum_k\frac{A_k}{1-e^{s_kT}z^{-1}}$$
实际上是将极点进行映射(零点就不会)
因此在进行转化的时候首先进行分式求和分解,然后直接转换,最后相加
可以看到,脉冲不变量法是设计数字滤波器一个非常好用的方法
下面两张图展示了该类变换的结果(其中有混叠的影响)
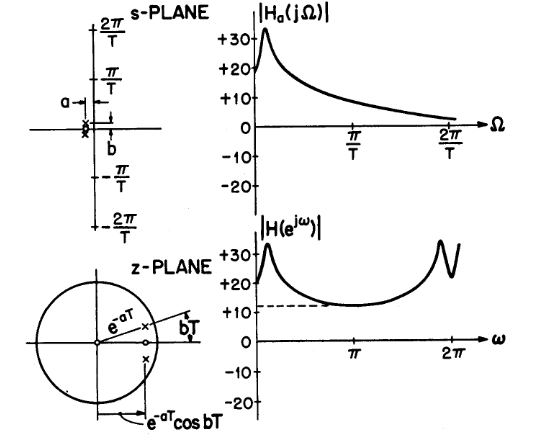
Bilinear变换法
我们也不是没有办法来处理这种混叠的情况,但也是有代价的
Bilinear变换
对于已知的函数$H_a(s)$,
我们取
$$s=\frac{2}{T}\left[\frac{1-z^{-1}}{1+z^{-1}}\right]$$
这是一个直接映射(与前面两种不同)
性质检验
- 对于$z=e^{j\omega}$,我们可以得到$z=j\Omega$(所以其满足频率响应相符)
下图展示了是如何实现映射的(我们可以注意到这里不会有混叠(因为整个轴映射到一个单位圆))但是这个频率响应会出现变形(就像最后一张图所示的一样)
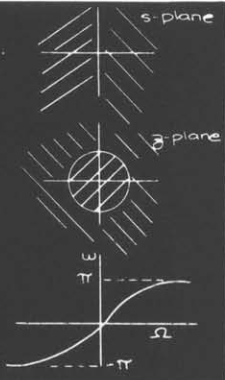
总体而言的效果像这样: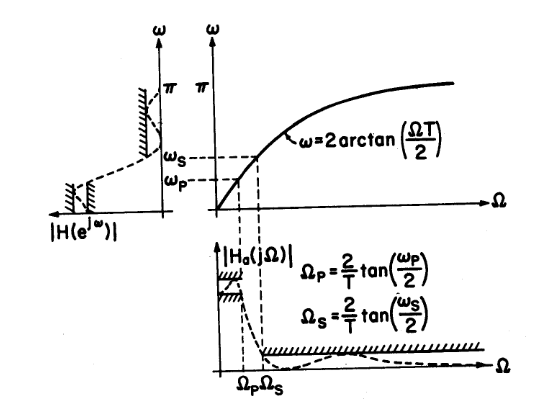
所以说,如果采样频率足够高,那么脉冲不变法要更加理想(不过主要是在低频上的效果不好)
代数设计法设计IIR
这些方法可以绕过设计模拟滤波器,直接进行设计
这种方法在响应谁都不知道的时候最为有用
最小平均方根误差法
这种方法看起来很复杂,但是实际上非常好理解
我们就是先搞一个理想的响应,然后用分式去拟合它

这里可以玩一点花,比如说我们要”特别照顾”一些频率,就可以用统计的方法提高其权重
最小平方逆
我们可以考虑指定脉冲响应
我们可以考虑一个理想状况下的响应的逆,然后两者一起作用,使结果最小
数字BUTTERWORTH滤波器
模拟BUTTERWORTH滤波器
定义为
$$|H_a(j\Omega)|^2=\frac{1}{1+(\frac{j\Omega}{j\Omega_c})^{2N}}$$
其中$\Omega_c$被称为截止频率,$N$为滤波器的阶数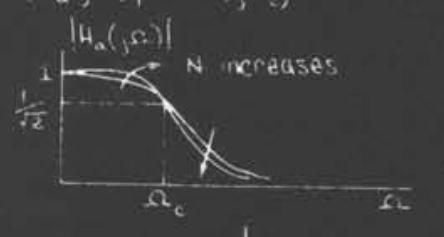
将其使用$S$代替,有(相当于从傅里叶变换变成拉普拉斯变换),则有
$$H_a(s)H_a(-s)=\frac{1}{1+(\frac{s}{j\Omega_c})^{2N}}$$
这个式子有极点,位于$s_p=(-1)^{\frac{1}{2N}}(j\Omega_c)$
分解开来,有
$$s_p=e^{j[\frac{\pi+2k\pi}{2N}]}e^{j\frac{\pi}{2}}\Omega_c$$
相当于在单位圆上等距分布的点,如图(ButterWorth圆)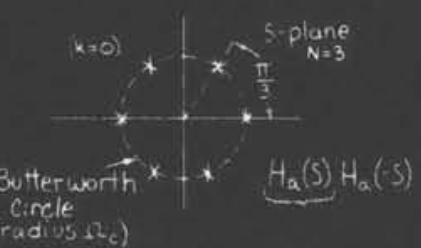
注意:这里我们的讨论仍然是在s平面上的,不要和z平面搞混
数字BUTTERWORTH滤波器
要求
我们让系统的转变点位于$0.2\pi$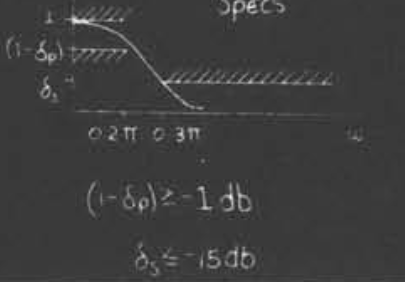
之后我们先用这些要求配合两种设计方法的特性得到相应的模拟滤波器
使用脉冲响应不变法设计
对于脉冲响应不变法,有
$$H(e^{j\omega})=\frac{1}{T}\sum_{k}H_a[\frac{j\omega}{T}+j\frac{2\pi k}{T}]$$
(设计的时候忽略混叠进行分析,$\Omega=\frac{\omega}{T}$为两种之间的关系)
我们可以得到如图所示的响应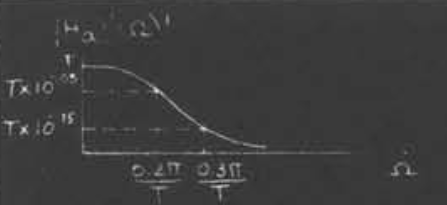
使用之前所定的条件,我们可以得到满足条件的要求$N=6$
首先求解$N$,然后向上取整,之后考虑到混叠效应,应当满足低频的方程
从而有$\Omega_c T=7032$
从而可以得到滤波器的形式(最终可以得到一个低通滤波器)
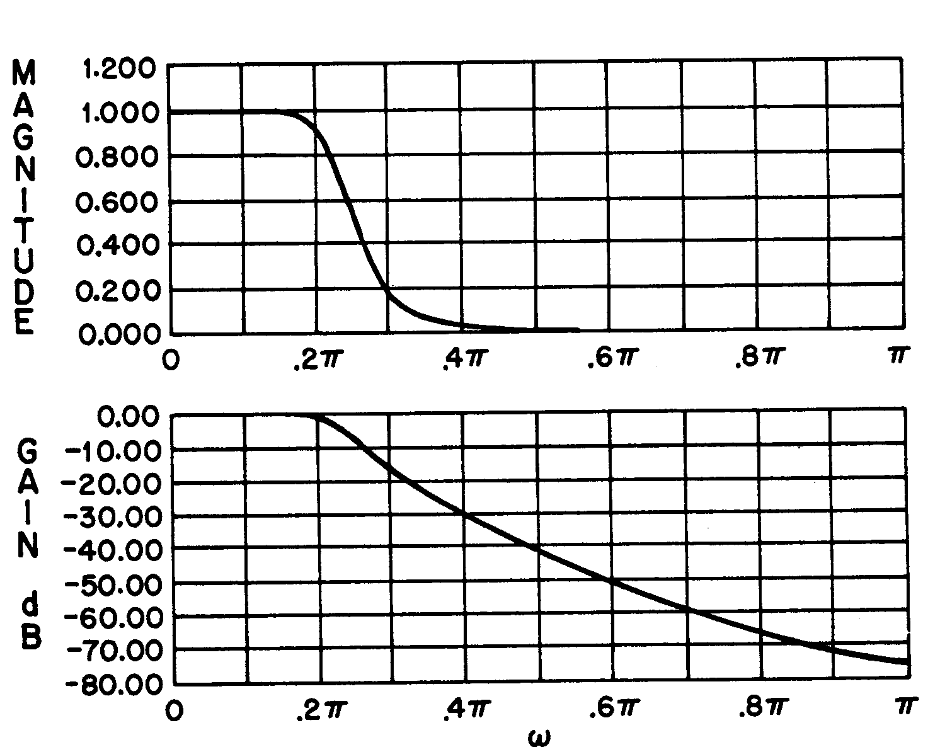
我们从这张图可以看出,在系统接近$\pi$的时候,整个滤波器的结果非常接近0
注意,我们这里是先设计模拟,最后一步转化被省略了
使用Bilinear变换法设计
由于Bilinear响应是非线性的,因此我们可以将两个核心的频率点映射到线上
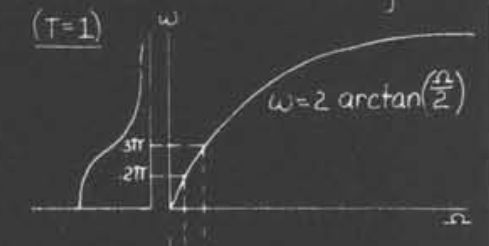
接下来我们就可以设计响应的模拟滤波器

在这里我们应当满足截止,因为在频率较高的时候线性性比较强
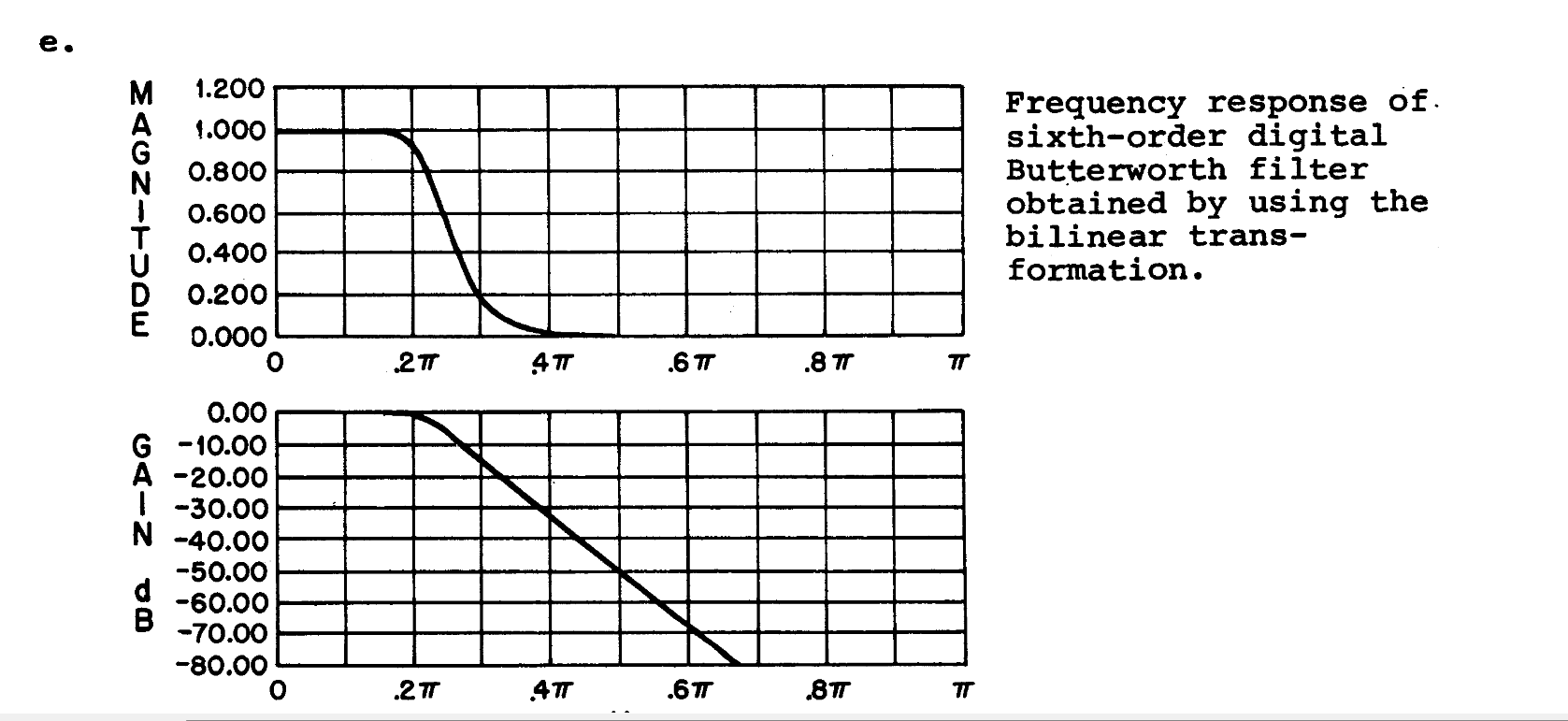
这种效果使得Bilinear在高频下工作更加理想
总结
我们可以通过两种数字滤波器不同的形式特点首先设计出相对应的模拟滤波器,然后再将其转化成数字滤波器,同时,由于我们的要求是对着数字滤波器提的,$T$可以认为是1
我们也可以通过一些手段让其变成高通或带通
例如:从低通($z$)变成高通($\alpha$)满足关系
$$z_l^{-1}=-\frac{z^{-1}+\alpha}{1+\alpha z^{-1}}$$
其中
$$\alpha=-\frac{\cos (\frac{\omega_1+\omega_2}{2})}{\cos(\frac{\omega_1-\omega_2}{2})}$$
FIR数字滤波器设计
我们之前讨论主要考虑将连续映射为离散,以及直接数学逼近的方法,在这一次,我们将讨论有限脉冲响应的数字滤波器
FIR滤波器的特点在于其良好的线性相位性质(要求$h(n)=h(N-1-n)),以及一些其他的优势
FIR数字滤波器的设计模拟滤波器要简单
主要有三种设计方法:
- 加窗
- 频率采样
- 等值涟波设计
加窗法设计的方式
一般我们希望设计的流程为:
- 考虑一个理想的响应
- 截断这个响应(使用窗)
而我们得到的频率响应则相当于信号与窗的卷积
例如,我们的理想频率响应为如下所示的形式: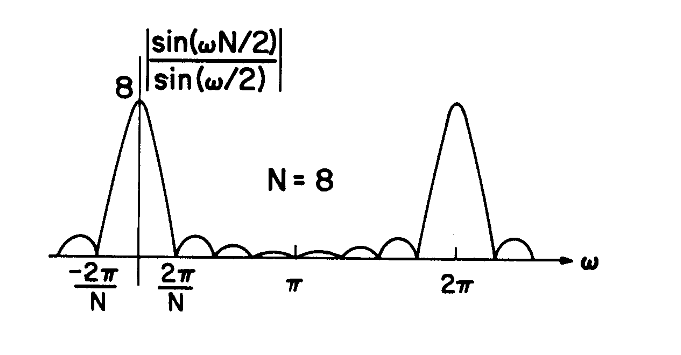
而我们添加一个矩形窗
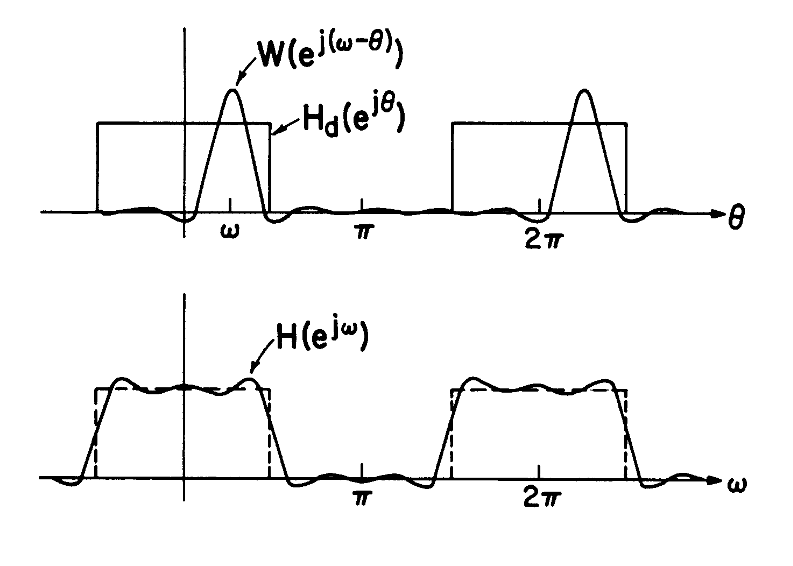
可以注意到,加窗后实线部分相较于理想状态下的存在涟漪
FIR越长,效果越好
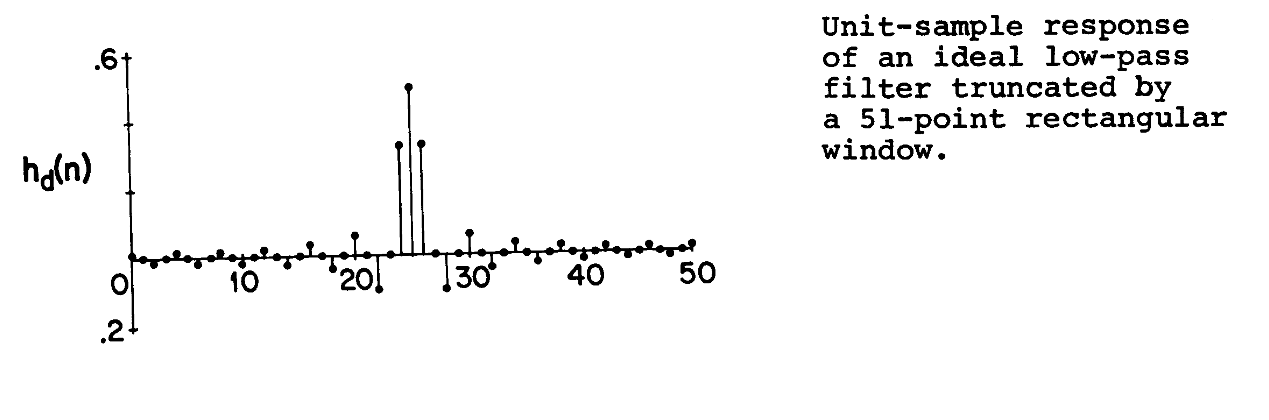
其加窗变换后的效果如图所示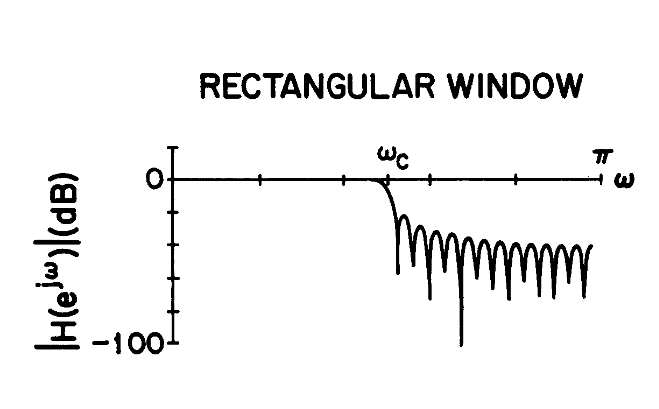
我们还可以加一些别的窗
HAMMING窗与BARTLETT窗
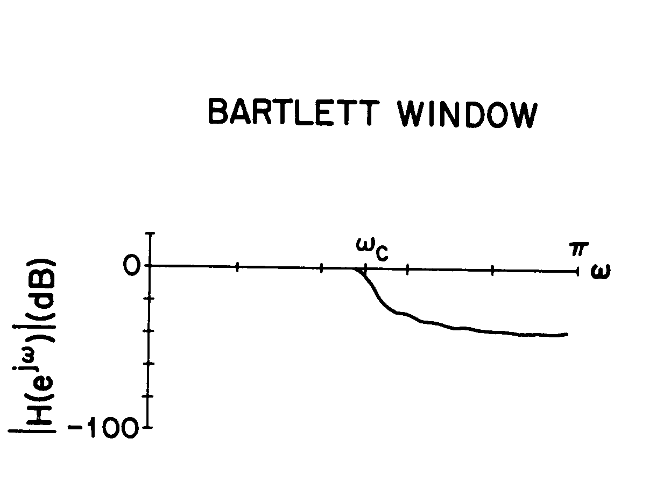
使用BARLETT窗,涟漪并不明显
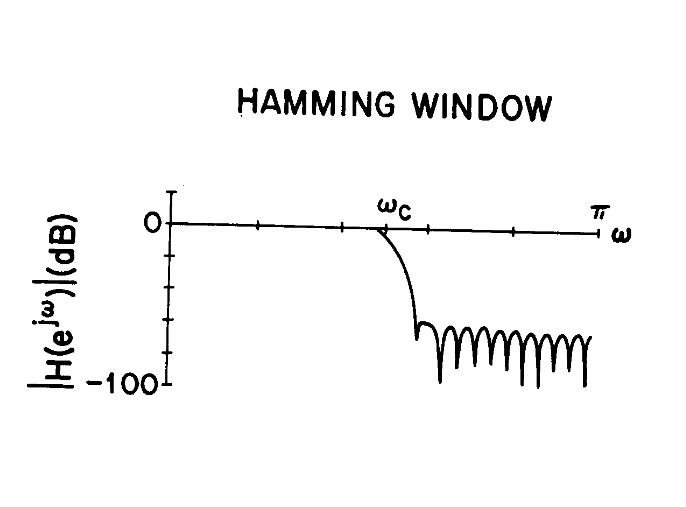
使用HAMMING窗,虽然转变带会大,但是抑制效果更好
频率采样设计
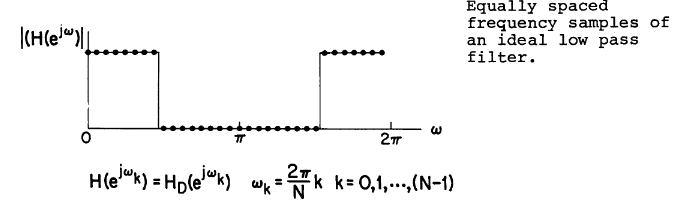
如果我们拥有一个理想的频率响应,那么我们可以使用频率采样的手段设计FIR滤波器去逼近
因此首先做DFT,然后再频率上等距取点,但是在这些点之间不一定性质良好,例如下图所示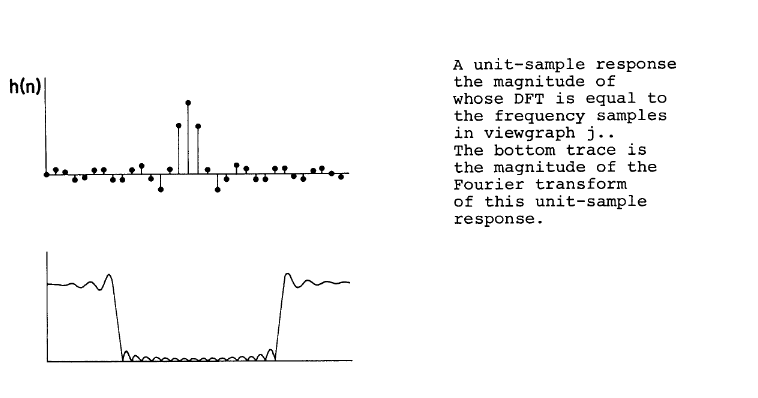
注意:傅里叶变换与离散傅里叶变换
离散傅里叶变换是有限响应长度的结果,而讨论其效果还得看傅里叶变换的结果
特别地,假如我们对冲击响应进行滚动平移,其DFT结果不变,但是傅里叶变换结果会发生改变
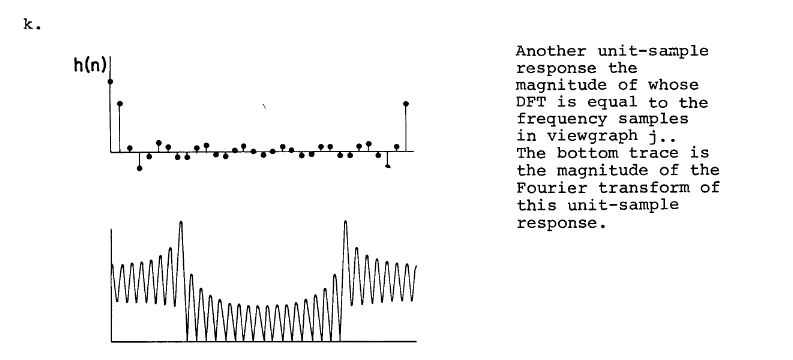
不过整体效果可能会变得非常奇怪
我们是否有方法减少涟漪?
我们可以考虑让边缘不需要那么窄的化,可以故意让边宽一点,然后实现较小的涟漪
等值涟波设计
例如,我们可以定义一些值,然后实现最小化计算