Songyuli's blog
0%

线性系统的性质和表示

Posted on Edited on Disqus:

线性系统

数字网络的表示

一个$N$阶线性差分方程,可以被表示为
$$y(n)=\sum_{k=1}^Na_ky(n-k)+\sum_{k=0}^Mb_kx(n-k)$$
此时$y(n)$可能是相关的(由边界条件决定),在此处我们认为其为相关的

基本操作的表示

延时

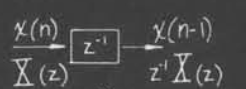
Alt text
将信号$x(n)$向后延时1就和在z变换域乘$z^{-1}$一样

数乘

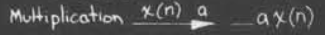
Alt text

相加

Alt text

如果涉及到许多信号的相加,可以考虑为树状形式

例子

下图展示了$y(n)=ay(n-1)+x(n)$的表示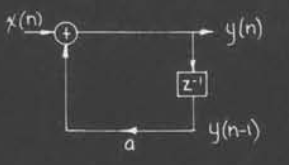
Alt text

信号流图

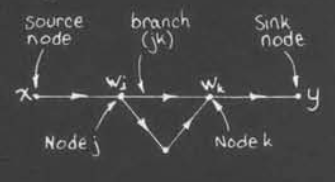
Alt text
对于每一个节点,都会有一个相应的变量,并且我们可以用节点来命名分支

信号流的结构

对于jk分支而言

  • 输入为$w_j$
  • 输出为$w_j$的函数

而对于一个节点,其值为输入分支的和

信号流图表示线性差分方程

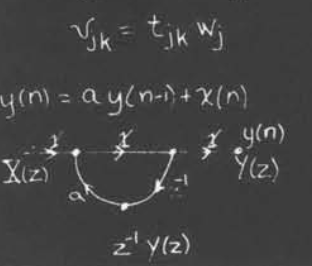
Alt text

一般而言,如果一个分支上面没有写倍率,默认为1

矩阵表示

前面我们讨论的是图像表示一系列线性方程,但是实际上我们使用的应当是其内部的代数结构

$$w_k(z)=\sum V_{jk}+\sum S_{jk}$$
前面一项可以视作输出”反馈”的结果,后面一项则是源的直接输入
进一步使用线性代数的方式表示,我们有如图所示的结果: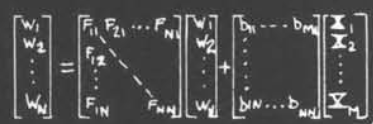
Alt text

因此我们可以使用矩阵写作
$$w(z)=F^T (z)w(z)+B^{T}X(z)$$

这里使用转置的原因是$F$的矩阵表示和其矩阵元的序号是前后相反的

注意,这里是在z空间中操作的

对于一阶的情况,我们可以将前半部分分解为$F^{T}(z)=F_C^Tw(z)+z^{-1}F^T_dw(z)$

相应的,如果我们将其转换到$n$空间中,我们可以得到
$$w(n)=F_C^Tw(n)+F^T_dw(n-1)+B^Tx(n)$$

不要忘记还有添加输入的$B$和如何输出的$C$

一个例子

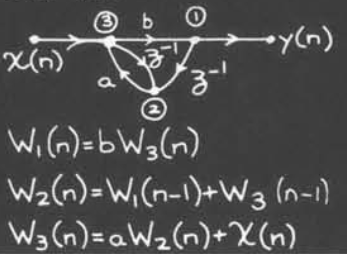
Alt text
我们可以将其重写为如下所示形式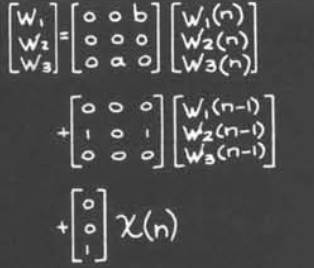
Alt text

而如果我们改变一下标号的顺序,我们可以得到流向图和矩阵表示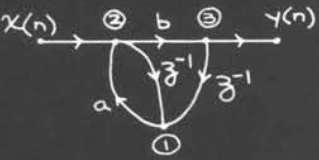
Alt text

我们可以注意到,按照这个顺序一个个来,那么每一个节点的结果都是可求解的

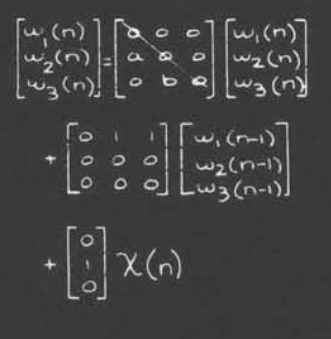
Alt text

我们可以注意到对于一个可计算的系统,其第一个矩阵的形式必须满足下三角
Alt text

对于每个节点间都有非延时连接的网络,其是不可计算的

这不代表其无法求解,只是无法序列求解

无穷脉冲响应系统的网络结构

对于一个相关的响应差分方程,我们可以得到其响应满足形式
$$H(z)=\frac{\sum b_kz^{-k}}{1-\sum a_kz^{-k}}$$
这个式子相当于分母为输入,分母为过去输出
得到的结果可以用下图表示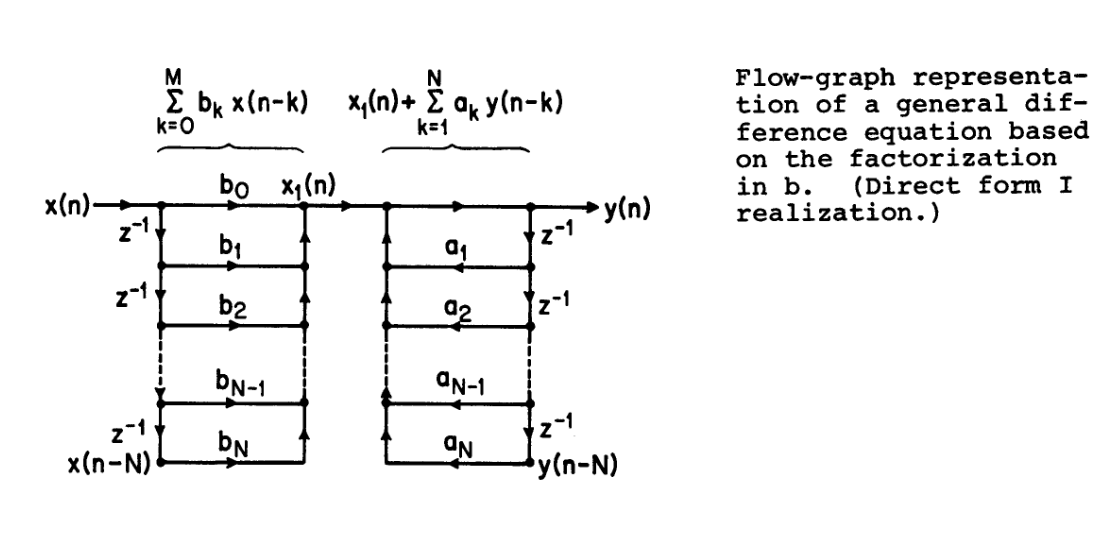
Alt text
相似的,我们可以改变作用的顺序而不改变结果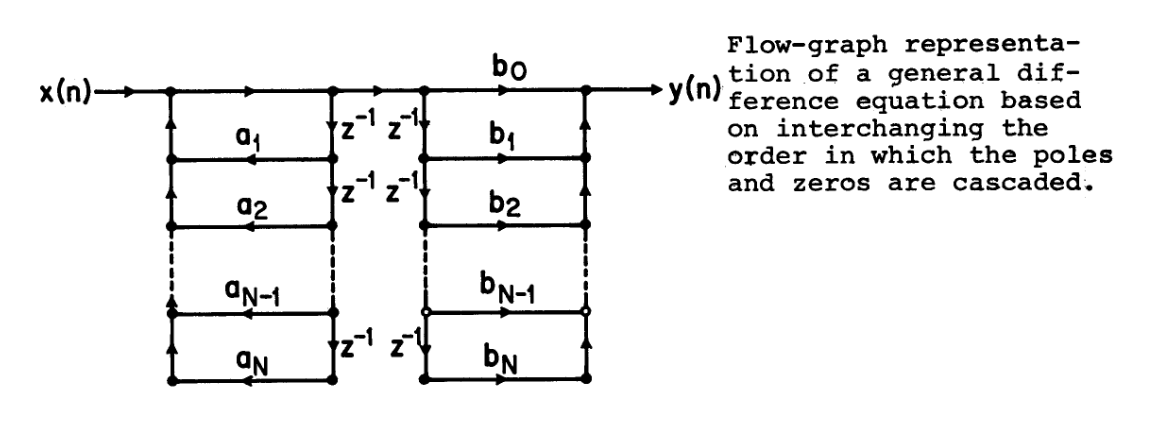
Alt text

但是这样做有什么样的好处

交换顺序的特点

我们在交换顺序后,可以相当于合并中间的分支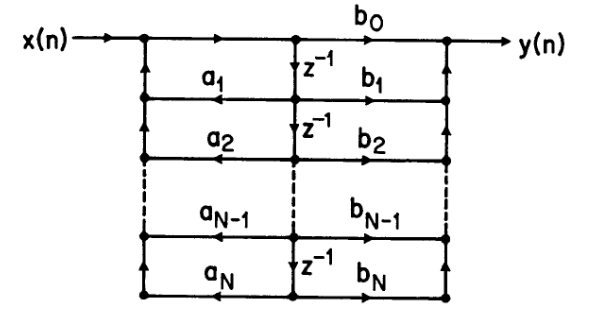
Alt text

我们相当于减少的运算

这里延时的次数是最大延时的值

转移理论

  1. 反转所有的分支
  2. 交换输入输出

那么同时执行两个操作后,转移函数保持不变
下图展示了从图一变到图二三的例子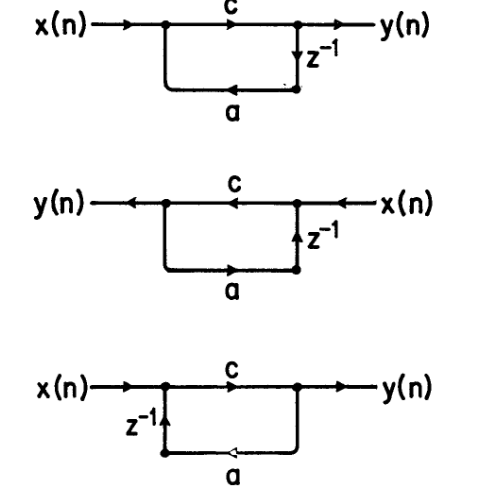
Alt text

相应的,我们也可以做出之前那张图翻转后的结果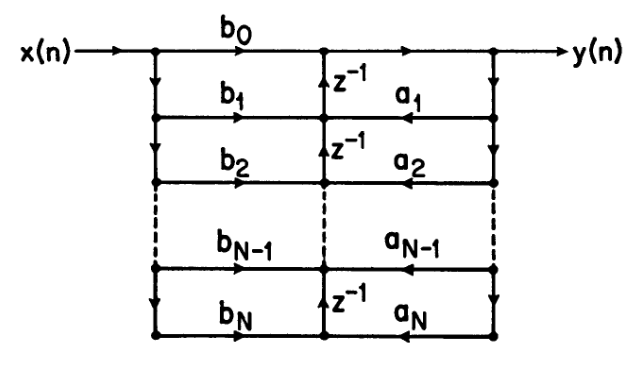
Alt text

瀑布结构

我们可以将原式进行多项式分解(分解成一系列二次项相乘)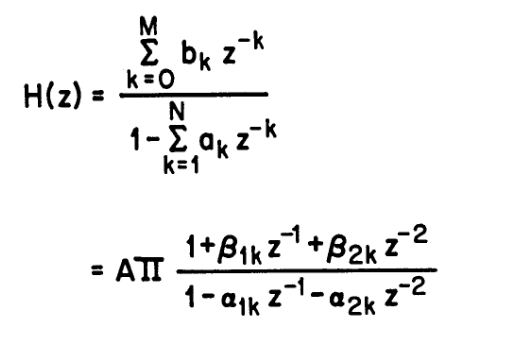
Alt text

我们这里采用二次项的原因是避免出现复数

这个相较于之前的表示能够使得参数的误差带来的影响没有那么严重

我们可以制作出相应的信号流向图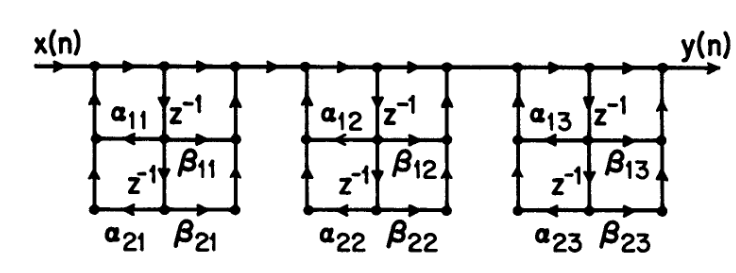
Alt text

并行结构

我们也可以将信号分解为一系列相加的形式
Alt text

下图展示了其效果(可以看出并行性)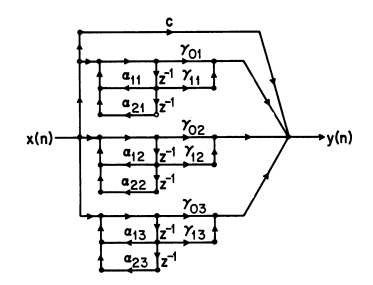
Alt text

使用并行结果,来自于一部分滤波器是直接得到极点与留数,因此要更为方便

不要忘记使用留数定理

FIR系统网络结构

FIR系统的结构

FIR系统只包含了一个有限多的求和,因此其可以表示为
$$y(n)=\sum_{k=0}^{N-1}h(k)x(n-k)$$
此图可以被表示为下图的形式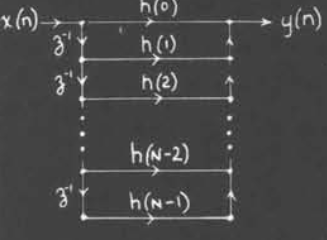
Alt text

线性相位FIR系统

我们可以考虑一个满足对称关系的系统结构$h(n)=h(N-1-n)$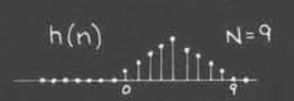
Alt text

我们需要注意,线性相位系统代表对于不同的频率输入,其相位变化是线性的
为了验证这个理论,我们可以构造一个偏移的相应(对应于$N$为奇数的情况)$Alt text$
我们可以注意到由于$h_1$是偶 函数,所以其频率响应是实函数,不产生相移.最终只会有产生$h_1$的一个位移

我们可以考虑一个系统,假设$N$是一个偶数,那么可以有
$$\sum_{n=0}^{\frac{N}{2}-1}h(n)z^{-n}+\sum_{n=\frac{N}{2}}^{N-1}h(n)z^{-n}$$
将其化简,我们可以得到
$$H(z)=\sum_{n=0}^3 h(n)[z^{-n}+z^{-(7-n)}]$$
画出相应的流向图就有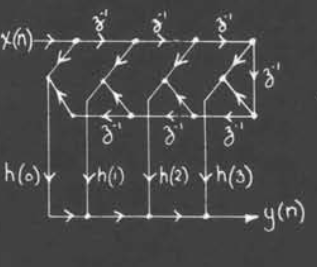
Alt text

这种配置只需要一般的乘法

频率采样结构

我们考虑一个有限相应结构,可以使用DFT和z变换表示

可以有
$$h(n)=\frac{1}{N}[\sum_{k=0}^{N-1}H(k)w_N^{-nk}]R_N(n)$$
进而得到z变换结果
$$H(z)=\frac{1}{N}\sum^{N-1}{k=0}H(k)\sum^{N-1}{n=0}\sum(z^{-1}w_N^{-k})^n$$
可以推导出

$$H(z)=(1-z^{-N})\frac{1}{N}\sum_{k=0}^{N-1}\frac{H(k)}{1-w_N^{-k}z^{-1}}$$
我们可以注意到等式左边为信号输出,而等式右边的系数则是系统的频率响应,因此,我们可以把这样的结构称为频率采样结构,其结构为

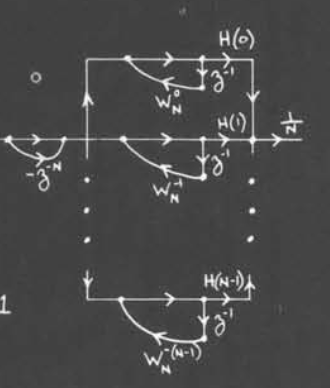
Alt text

需要注意到的是,这里的系数是复数,在实际运用中还需要做一些操作

这里有一个有趣的性质:式子里面有极点,但最后的输出没有极点(因为里面约去了)

虽然看起来这个非常复杂,但是对于现实的系统(例如一个窄带滤波器),大部分的频率响应都是0

这里还有一个好处,对于不同的$H(k)$,我们不需要单独制作环,可以实现高度共享

有限长寄存器的特点

  1. 数学计算的位数是有限的(会发生截断)
  2. 参数也会被截断

参数量子化简述

例如我们考虑一个系统
$$H(z)=\frac{B(z^{-1})}{A(z^{-1})}$$
其中可以表示为
$$A(z^{-1})=\Pi(1-z_kz^{-1})$$
之后考虑存在误差
$$a’_k=a_k+\Delta_k$$
那么我们可以计算得到以下结果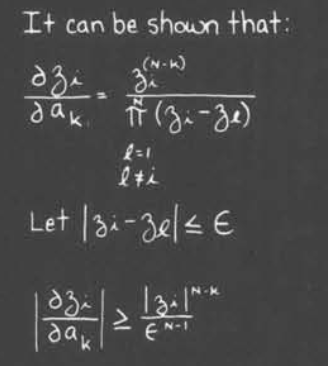
Alt text

这意味着如果极点次数越高,那么固定的误差越大,输出误差越大
所以我们应当减少次数

同时,即使在同样的大结构中,不同零点-极点的配置也会带来区别,我们至少要注意到这样的问题