离散傅里叶级数
对于大部分情况,傅里叶变换和z变换是初等的变换,但是必须要处理无限长的情况,这在实际情况中不太现实
离散傅里叶变换有着与傅里叶变换相似的性质,但是也有着显著的区别,但是在实际的应用中会直接使用到离散傅里叶变换
其主要思想是:使用傅里叶变换的采样来描述一段有限长的序列
使用周期序列介绍离散傅里叶级数
首先考虑一个有限长的$x(n)$序列,总长度为$N$
这里是至小于0或者大于$N-1$的序列值均为0
我们可以周期延拓这个序列,得到$x’(n)=x(n)+x(N+n)+…$
我们可以在有限长度序列和周期序列之间相互转换
这里的效果就像把输入序列放在油漆刷上,然后一遍遍涂出来的效果
将周期序列乘上一个矩形门就可以得到原始的序列
做这个延拓的意义在于:既然在连续的情况下,周期序列有傅里叶级数表示,离散也应当类似,于是可以得到离散傅里叶变换(DFT)的定义:
$x’$的离散傅里叶级数就是$x$的离散傅里叶变换
$$x’(n)=\sum X’(k)e^{j\frac{2\pi}{N}nk}$$
其中$X’(k)$是展开系数($k$与$n$都是离散的)
离散傅里叶级数的特性
我们可以注意到不仅仅$n$是周期的,$k$也应当是周期变化的
所以我们可以得到一个求和区间$\sum_{k=0}^{N-1}$
我们同样也可以用一个关系得到其系数的计算
$$X’(k)=\sum_{n=0}^{N-1}x(n)e^{-j\frac{2\pi}{N}nk}$$
这里的$k$是有有限多个值,相应的$X’(k)$也是有有限多个值
$x(n)$是周期的,相应的$X(k)$也是周期的
为了简化表示,我们可以记$w_m=e^{-j2\pi/N}$,那么原来的式子就可以被表示为
$$x’(n)=\frac{1}{N}\sum X’(k)w_N^{-nk}$$
$$X’(k)=\sum x’(n)w_N^{nk}$$
离散傅里叶变换的特性
在时域上的特性,我们也会在频域上找到,这是离散傅里叶变换特别的特性
频移
$$x(n+m)\lrArr w_N^{km}X(k)$$
$$w_N^{ln}x(n)\lrArr X(k+l)$$
对称性
这个和傅里叶变换的结果相似,在这里不再介绍
卷积性质
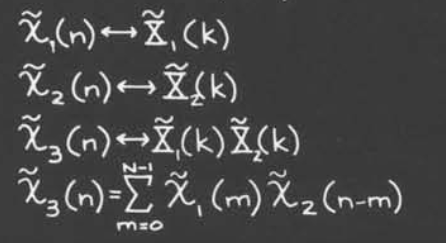
下图可以看到卷积性质的应用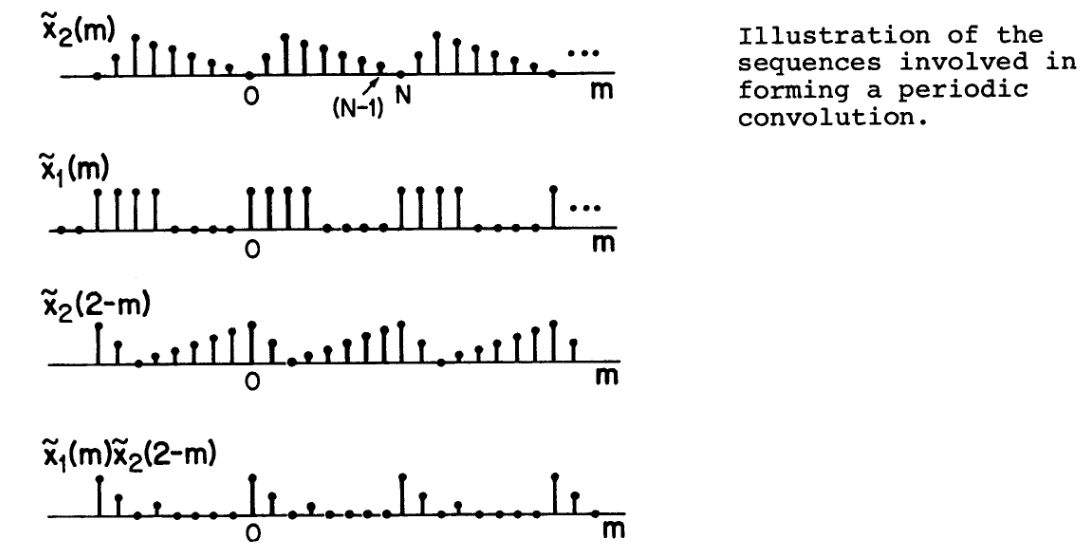
总结
我们在这里可以仅仅通过有限多的频率信息得到有限长度序列的信息
离散傅里叶变换
我们之前讨论了循环序列的离散傅里叶级数,(用有限多个数表示)
$$x’(n)=x(n mod N)=x((n))_N$$
我们这里使用余数来描述沿伸的信号
其中离散傅里叶级数表示为
$$X’(k)=\sum_{n=0}^{N-1}x’(n)w_N^{nk}$$
$$x’(n)=\frac{1}{N}\sum X’(k)w_N^{-nk}$$
离散傅里叶变换
我们令$X(k)=\sum_{n=0}^{N-1}x(n)w_n^{nk}$($k=0,1,…,N-1$)
这样我们就同样拥有一个有限长的傅里叶变换
我们可以看出来这里的离散傅里叶变换结果和信号序列的效果几乎完全一样
同样也有$X(k)=X’(k)Q_N(k)$,$X’(k)=X((k))_N$
因此我们可以得到离散傅里叶变换的关系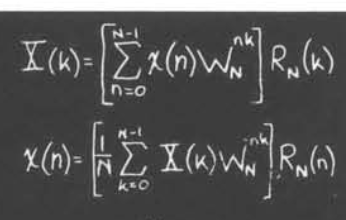
相应的,对于z变换,DFT可以视作为z变换的一种采样
离散傅里叶变换性质
这里我们主要注意到离散变换和连续变换之间的区别(始终记住作用是针对周期信号而言的)
平移性质
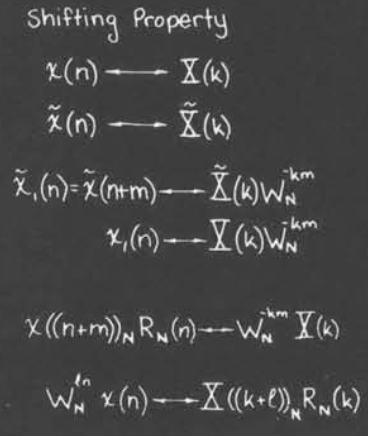
我们需要注意,这里的平移不是简单的$n$移动,而是像如图所示的那样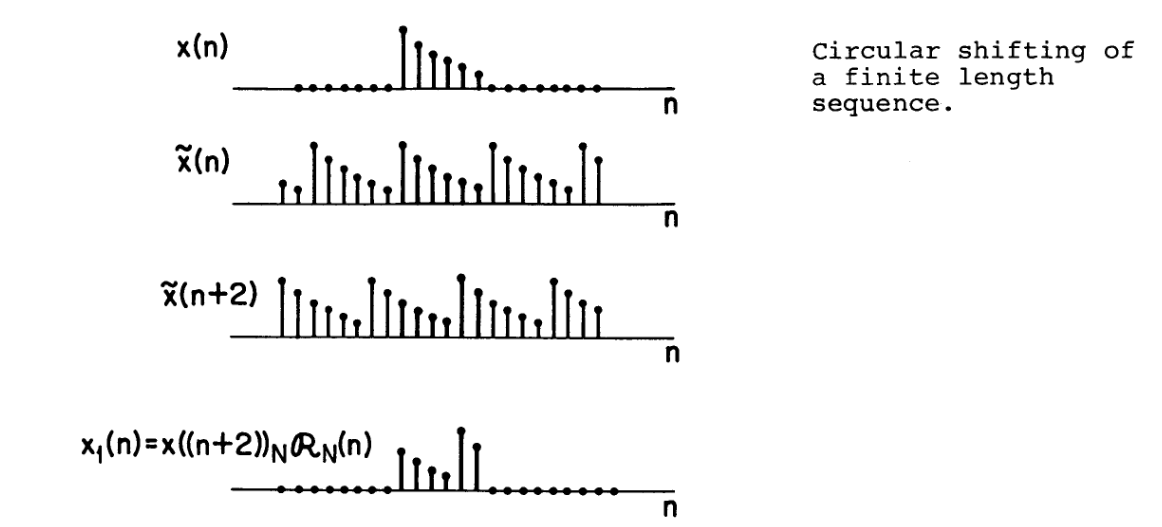
这里是把后面的移动到了前面来(就像之前所说的”圆柱体”一样)
对称性
这个性质讨论的是有关于实信号的结果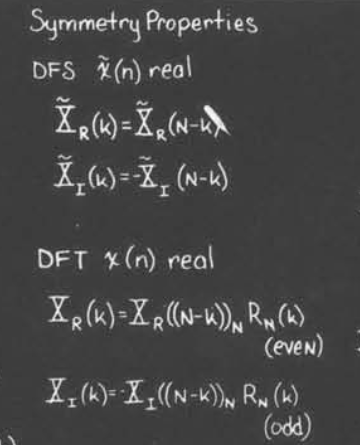
这里的变换在运算时需要转化为周期的级数来处理
下图展示了这一性质的效果
卷积性质
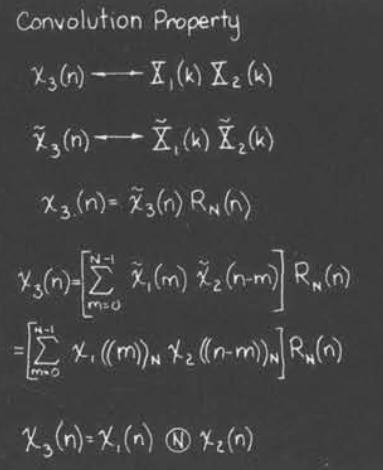
这里需要注意到卷积的原始定义发生了变化
不过实际上循环卷积非常丰富,其主要的意义将在后面一节阐明
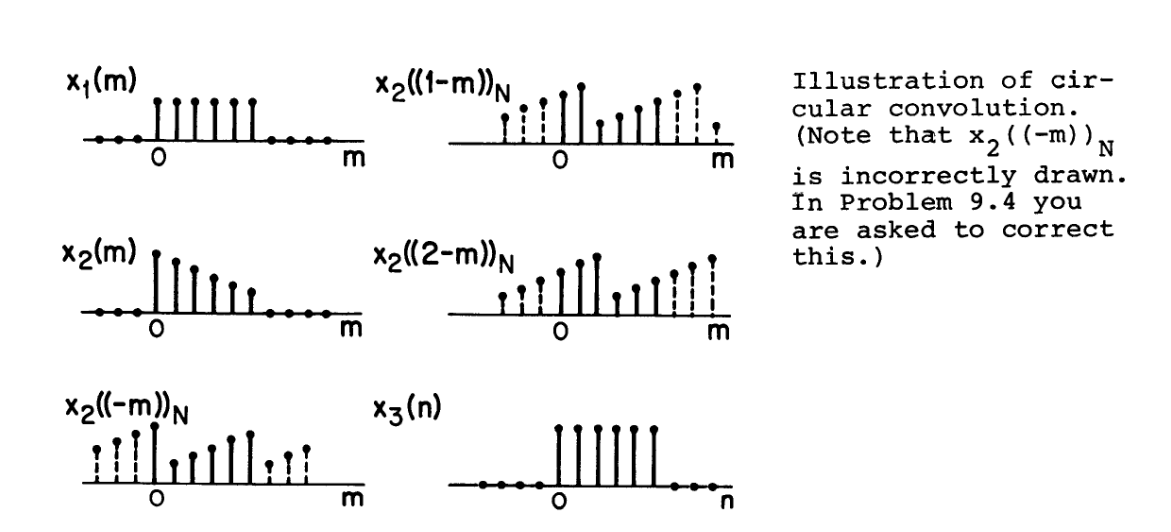
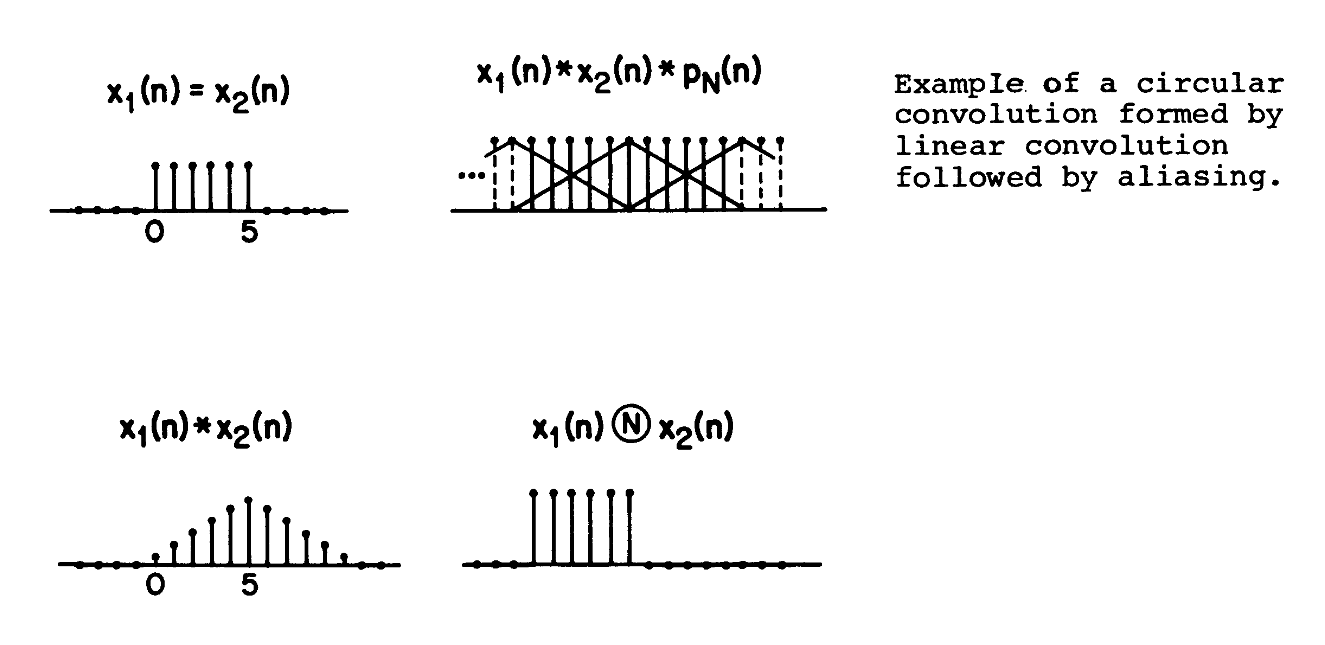
下图展示了循环卷积的一个例子
环路卷积
由于FFT的存在,因此卷积实际上非常的方便
卷积性质的复习
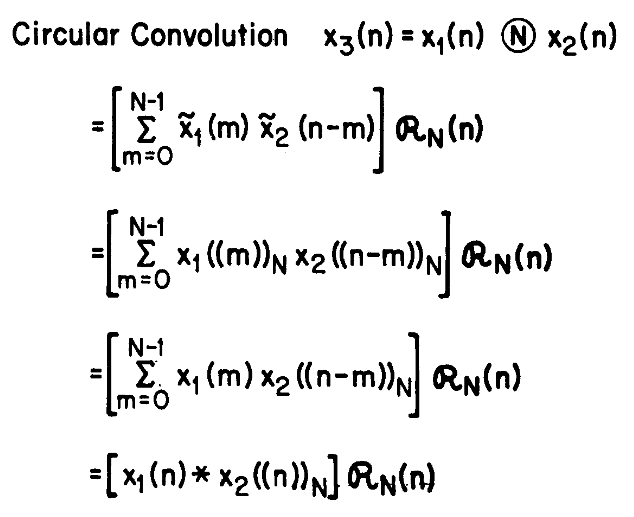
注意,首先要把序列变成重复序列(或者用取模序列)
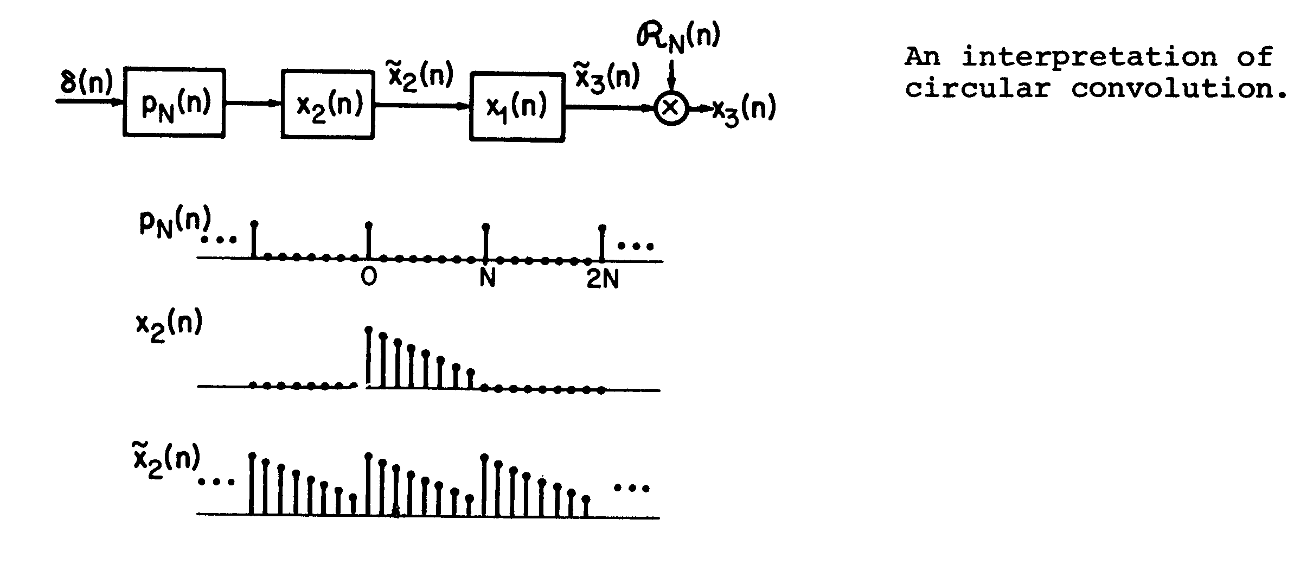
最后一个式子可以理解为将$x_2$与一个周期脉冲相互卷积,然后再和$x_1$卷积
就像这张图中所展示的一样
下图则展示了像这样的操作是如何被计算出来的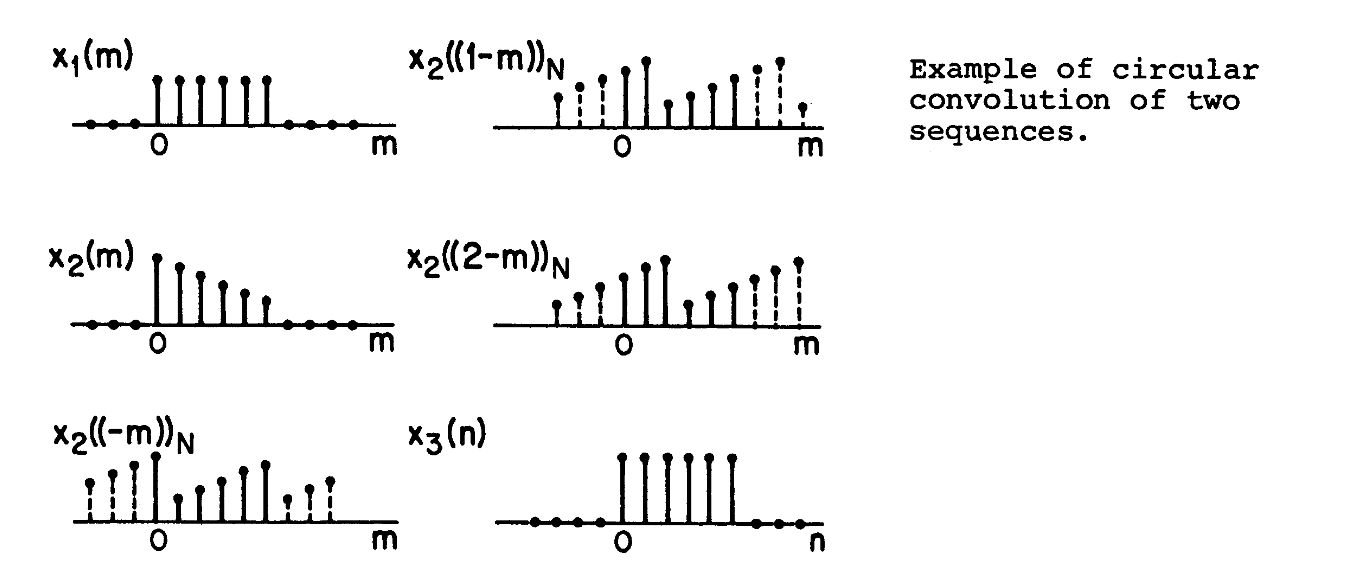
有关卷积的有趣的解释
如果我们看如下所示的两个系统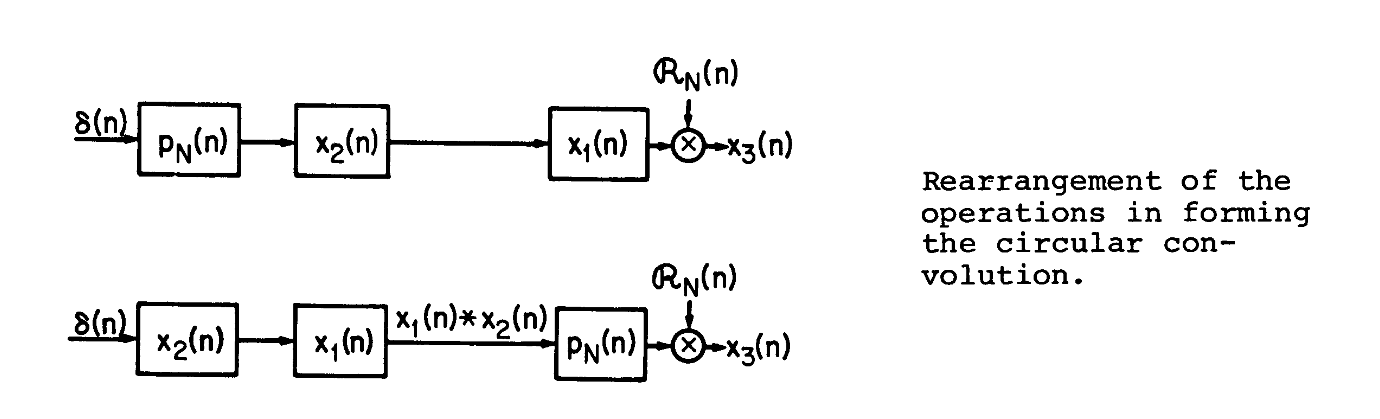
这意味着我们可以首先用两段信号相应的线性卷积通过一个单位相应是间隔为$N$的脉冲序列得到两段信号的环路卷积
我们可以得到一个重要的结论
环路卷积可以被视作线性卷积与混叠共同作用的结果
如果将$x’3(n)$看作为线性卷积,那么我们可以有关系
$$x_3(n)=[\sum{r}x’_3(n+rN)]R_N(n)$$
注意一下,这里的形式和离散傅里叶变换有着异曲同工之处
一些例子以及如何从循环卷积得到线性卷积
如果我们将周期变成$2N$,那么又会有什么样的变化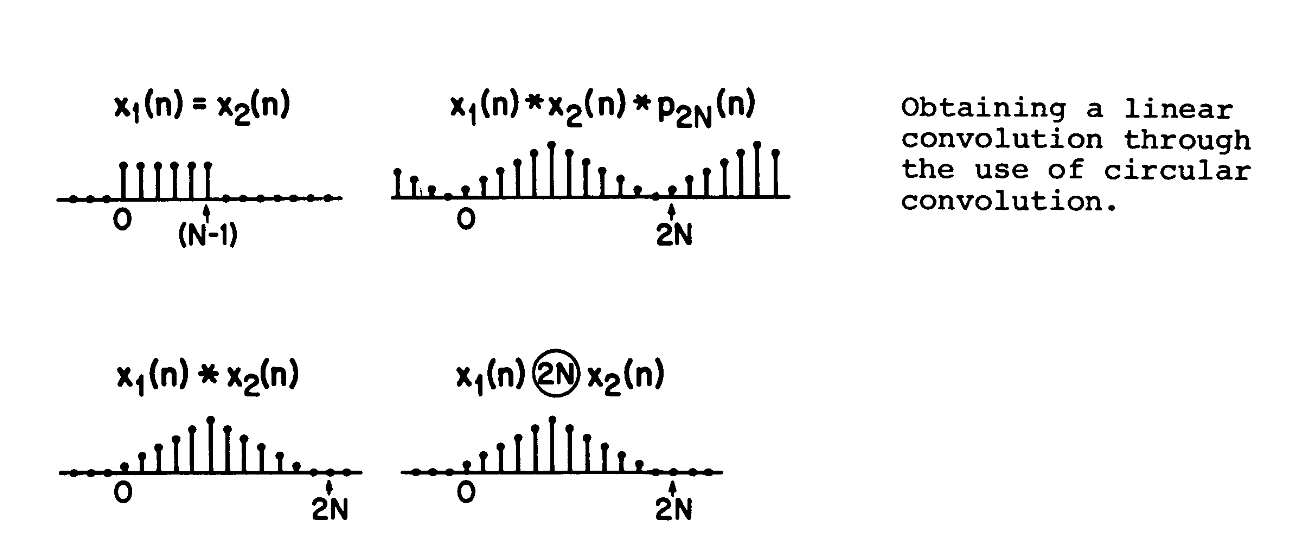
可以注意到,混叠的效果消失了
如果我们在处理信号的时候,我们就需要避免循环卷积,所以需要多一段0(总的处理点数应该是信号点数加上单位响应)
信号的分段
目前我们所讨论的问题针对与滤波器已经知道整个序列的前提之下,但是实际上,这种情况很难实现
以下面一个例子为例,我们可以将输入的信号分成$L$为段的信号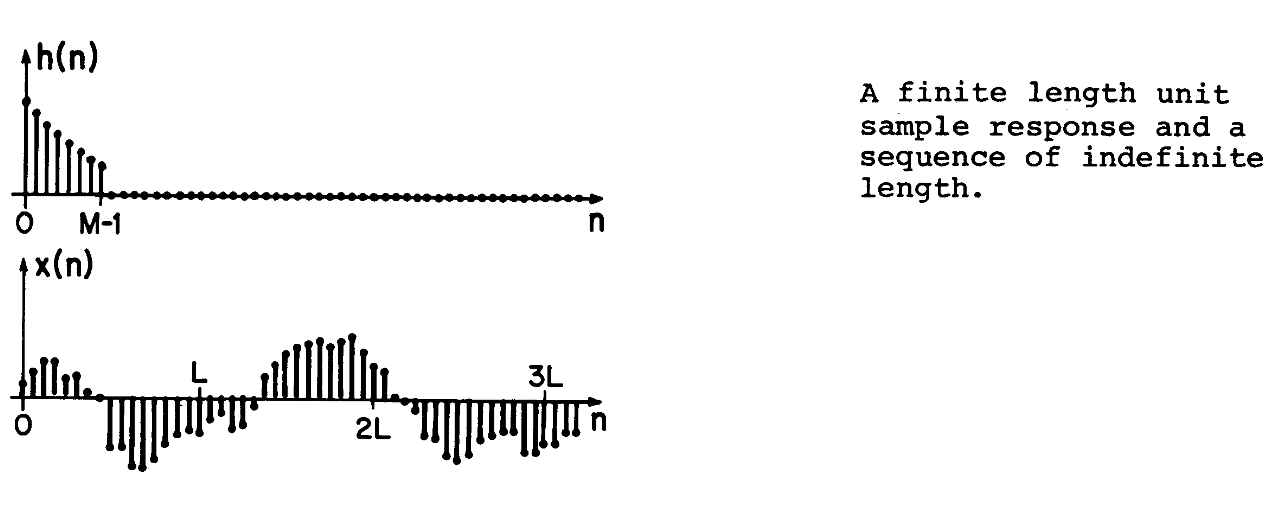
经过转化后,我们有这样几段信号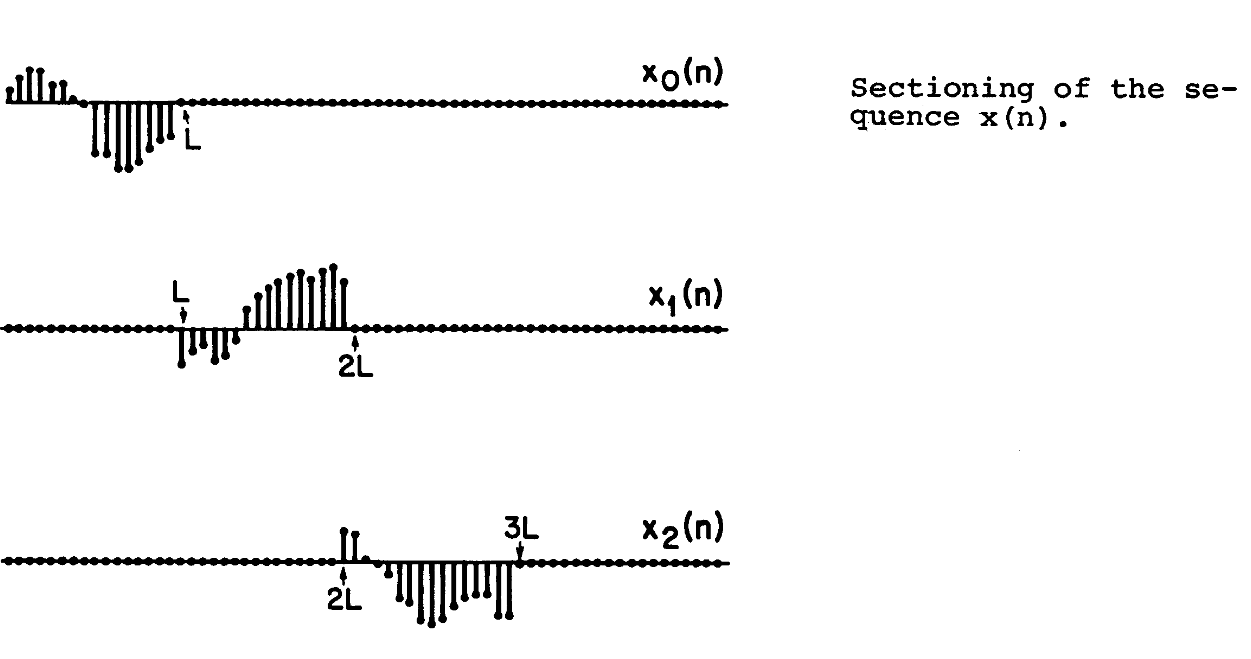
经过卷积(这里虽然是循环卷积,但由于填的0足够长,所以就是线性卷积),我们可以得到以下结果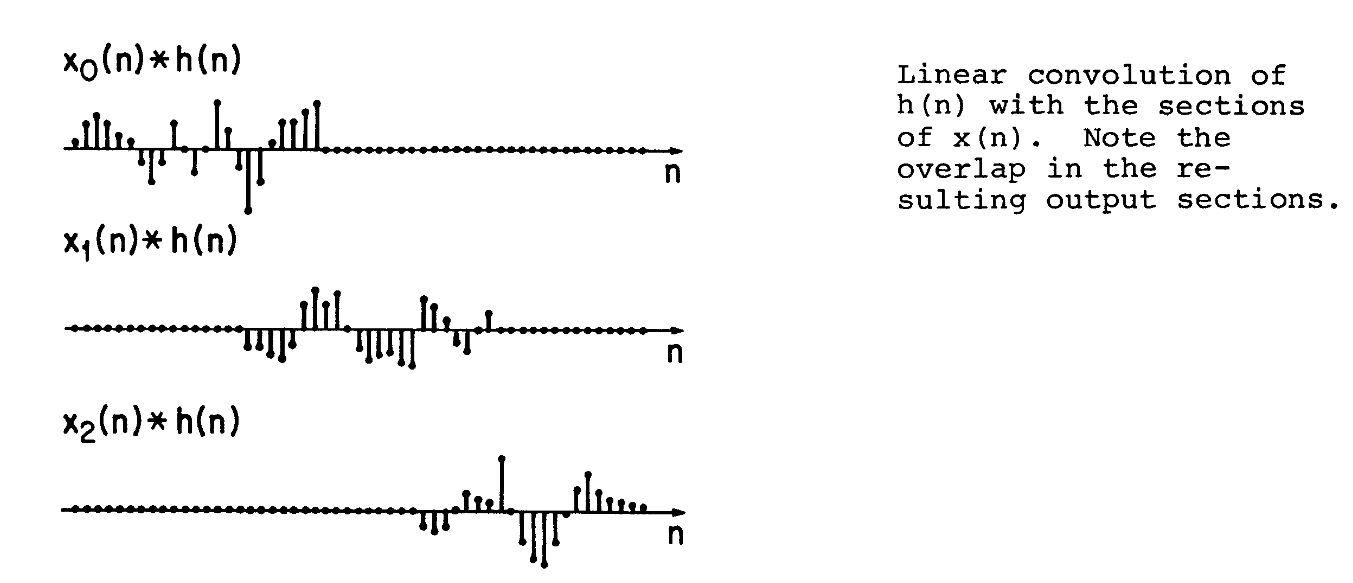
最后将其叠加到一起即可
总结
由于我们将会有非常高效的方法进行DFT(FFT),所以一般信号处理所使用的卷积可以使用DFT来处理
然而,由于DFT的卷积定理是使用环路卷积实现的,所以我们需要填0来实现线性卷积的表示