1
2
3
4
5
6
7
8
9
10

import pandas as pd
from io import StringIO

csv_data=\
    '''A,B,C,D
    1,2,3,4
    5,6,,8
    10,11,12,'''
df=pd.read_csv(StringIO(csv_data))
df

处理缺失值的前提自然是找到缺失值,但是在一个可能非常巨大的CSV文件里面人工去找缺失值很不现实,我们可以使用isnull来将一个DataFrame转化为相应的布尔数组

1

df.isnull().sum()

A    0
B    0
C    1
D    1
dtype: int64

可以看到,C列和D列各有一个缺失值

需要注意到的是,DataFrame更加适合于数据的处理,但是机器学习所用的数据往往是以Ndarray的形式出现的,我们可以使用df.values实现这一转换

删除具有缺失值的样本或特征

对付缺失值,最简单的方法莫过于是直接将其删除,我们可以使用dropna将存在缺失值的行或列删除

1

df.dropna(axis=0)

1

df.dropna(axis=1)

当然,dropna也支持其他选项,下面有几个比较重要的

1

df.dropna(how="all")#只有全部缺失才删除

1

df.dropna(thresh=4)#删除有效值小于4个

1

df.dropna(subset=['C'])#只考虑C列的nan要删除

虽然删除缺失值非常方便,但也伴随着一些问题,我们可能会丢失太多的数据.
因此,我们接下来要看看最为常用的内插法处理缺失值的方法

计算缺失值

一般而言,将缺失值全部去掉并不现实,我们这里则是采用内插处理

在内插中最为常见的莫过于平均值内插,我们就将缺失值替换为整个特征的平均值,这么做有一个简单的方法就是使用Imputer类,就像下面所展示的那样

1
2
3
4
5
6

from sklearn.impute import SimpleImputer#!0.22版本以上需要使用SimpleImputer代替
import numpy as np
imr=SimpleImputer(missing_values=np.nan,strategy='mean')
imr=imr.fit(df.values)
imputed_data=imr.transform(df.values)
imputed_data

array([[ 1. ,  2. ,  3. ,  4. ],
       [ 5. ,  6. ,  7.5,  8. ],
       [10. , 11. , 12. ,  6. ]])

可以注意到,每一处的NaN都已经被相应的平均值所替换了,这种手段在分类数据中非常有用

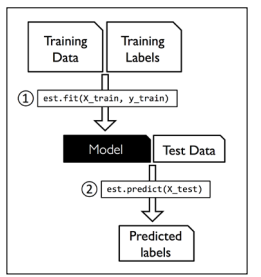
理解scikit-learn中的估计API

在之前的部分中,我们采用SimpleImputer类来计算我们数据集中的缺失值,这在scikit-learn类中被称作转换类
转换类中最为重要的两个方法就是fit和transform,实际上,这和我们之前所学的分类数据很像,主要区别在于我们这里的训练集和测试集都要经过相同的处理(但是fit过程还是要用训练集),如图所示:

处理分类数据

到目前为止,我们处理的还主要是数值数据,但是在现实生活中一个或多个分类数据并不少见,在这一部分,我们将用一些简单而有效的例子来展现我们应当如何处理这类数据.

可排序与不可排序的特征

如果我们在讨论分类数据时,我们往往会进一步将其分为可排序和不可排序的特征

可排序特征比如我们可以认为超大号>大号>中号>小号来对衣服尺码的分类来进行排序,但是显然我们无法对一些特征例如男性或女性这样的特征进行排序

创建一个示例数据集

在我们探索处理这样的分类数据前,我们首先先创建一个用来展现问题的数据集

1
2
3
4
5
6
7
8

import pandas as pd
df=pd.DataFrame([
    ['green','M',10.1,'class1'],
    ['red','L',13.5,'class2'],
    ['blue','XL',15.3,'class1']
    ])
df.columns=['color','size','price','classlabel']
df

我们可以看到,刚刚创建的DataFrame包含一个不可排序的特征,一个可以排序的特征
而分类标签则是被储存在了最后一列
在我们所使用的学习算法中,并不会使用到标签的先后顺序

映射可排序特征

为了保证学习算法可以准确地解释排序特征,我们需要将分类标签字符串转化为整数
不幸的是,没有可以从标签直接方便地转变成数字的方法,因此我们需要手动去定义映射

1
2
3
4
5
6
7

size_mapping={
    'XL':3,
    'L':2,
    'M':1
}
df['size']=df['size'].map(size_mapping)
df

可以看到size特征已经被完全地分割了,而假如最后我们希望其再替换回原来的字符串标签,我们可以使用制作一个反映射字典,其做法并不困难,用生成器非常方便

1
2

inv_mapping={v:k for k,v in size_mapping.items()}
df['size'].map(inv_mapping)

0     M
1     L
2    XL
Name: size, dtype: object

编码类标签

许多机器学习库需要编码成正整数的类标签(虽然也有很大一部分在内部执行这一工作)
为了给类标签编码,我们可以用前一部分的方式,但是我们同样也要记住,此处的标签是不可排序的,因此我们只需要简单地枚举类标签(从0开始)

1
2
3

import numpy as np
class_mapping={label:idx for idx,label in enumerate(np.unique(df['classlabel']))}
class_mapping

{'class1': 0, 'class2': 1}

接下来,我们就可以将类标签转换为整数

1
2

df['classlabel']=df['classlabel'].map(class_mapping)
df

我们也可以像之前那样翻转键值对以达到返回原来表示形式的目的

1
2
3

inv_mapping={v:k for k,v in class_mapping.items()}
df['classlabel']=df['classlabel'].map(inv_mapping)
df

相应的,在机器学习库中也有一个LabelEncoder类也可以直接实现这个目的

1
2
3
4

from sklearn.preprocessing import LabelEncoder
class_le=LabelEncoder()
y=class_le.fit_transform(df['classlabel'].values)
y

array([0, 1, 0])

需要注意的是fit_transform就是简单地先后依次调用fit和transform,接下来我们可以使用inverse_transform将整数类标签再转换为原来的字符串表示

1

class_le.inverse_transform(y)

array(['class1', 'class2', 'class1'], dtype=object)

在不可排序特征使用”单一热源”(one-hot)编码方式

在我们之前的部分中,我们采用的是一个简单的字典映射的方法进行编码
但是这存在一个问题,倘使我们采用这样的编码形式,那么即使我们认为各个数之间不存在大小关系,但是学习算法不会那么想,这会导致一些错误

一种常见的解决方法是采用一种被称作”单一热源编码”(one-hot)的方式,其原理是为每一个特定的分类创建一个新的特征

比如说颜色,从原来的颜色(红绿蓝),变成三个特征(是否是红,是否是绿,是否是蓝)

我们可以使用OneHotEncoder实现这个功能

1

df[['color','size','price']].values

array([['green', 1, 10.1],
       ['red', 2, 13.5],
       ['blue', 3, 15.3]], dtype=object)

1
2
3

from sklearn.preprocessing import OneHotEncoder
ohe=OneHotEncoder()
ohe.fit_transform(df[['color']].values).toarray()

array([[0., 1., 0.],
       [0., 0., 1.],
       [1., 0., 0.]])

需要注意一下,如果我们希望在这里对于一整个数据集中的部分类施加这一方法,在书中的版本中,采用的是categorical_features这一关键字参数,但是这个参数在现在的版本中已经被废除,因此应当采用以下形式

1
2
3
4
5

from sklearn.compose import ColumnTransformer
X=df[['color','size','price']].values
color_en=ColumnTransformer([("Test Transform",OneHotEncoder(),[0])],remainder='passthrough')
X=color_en.fit_transform(X)
X

array([[0.0, 1.0, 0.0, 1, 10.1],
       [0.0, 0.0, 1.0, 2, 13.5],
       [1.0, 0.0, 0.0, 3, 15.3]], dtype=object)

当然,我们处理这个还有更加方便的方法,就是使用get_dummies方法(pandas内置)

1

pd.get_dummies(df[['price','color','size']])

注意,这个方法只会修改以字符串为内容的列,其他列不变

将数据集分割成训练集和测试集

我们之前曾经简单描述过如何将训练集进行分割,在这一部分,我们将准备一个全新的测试集Wine,这里面有178个酒类数据,每个有13个特征

1
2
3

df=pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data"
               ,header=None)
df

将这个分割成分别的训练集和测试集是使用train_test_split函数

1
2
3

from sklearn.model_selection import train_test_split
X,y=df.iloc[:,1:].values,df.iloc[:,0].values
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3,random_state=0,stratify=y)

在这一步中,我们首先将数据中的特征与分类标签区分开来,然后随机划分30%的测试集,向stratify参数中输入标签是为了保证三种不同的标签都等量的被选中

我们需要注意到,应当尽量避免出现在划分数据集时去掉了有价值的内容,因此,我们可能要选取多次划分

将特征归一化

在我们的处理流程中,特征重放缩是一个非常容易被忘掉,但是也非常重要的一步.只有非常少见的算法(决策树和随机森林)不需要考虑重放缩的问题
这里我们利用梯度下降法进行机器学习来展示这种技术的效果

归一化的效果非常容易想象,比如有两个特征,一个范围01,一个范围010000,那么如果我们不进行归一化,毫无疑问,算法会主要处理后面那个特征.

而对于将不同的特征带到同样一个范围有两种常用的方式:归一化(normalization)和标准化(standardization),但这两种说法经常被混用,需要注意.往往归一化是将特征转换到[0,1]的范围中,使用的叫最大-最小缩放,计算公式也非常简单
$$x_{norm}^{(i)}=\frac{x^{(i)}-x_{min}}{x_{max}-x_{min}}$$
代码则如下所示

1
2
3
4

from sklearn.preprocessing import MinMaxScaler
mms=MinMaxScaler()
X_train_norm=mms.fit_transform(X_train)
X_test_norm=mms.transform(X_test)

虽然这种最大-最小放缩在我们已知范围的数据区间内非常有用,但是标准化在许多机器学习内容中更加重要,尤其是优化算法比如梯度下降法.通过标准化,我们可以将特征集中到以0为均值,1为标准差的方位之内.
另外,标准化还有一个很大的好处,就是它不是那么容易受到极值的影响
标准化的流程可以用下式来表示:
$$x_{std}^{(i)}=\frac{x^{(i)}-\mu_x}{\sigma_x}$$
我们可以使用以下代码来执行标准化过程

1
2
3
4

from sklearn.preprocessing import StandardScaler
stdsc=StandardScaler()
X_train_std=stdsc.fit_transform(X_train)
X_test_std=stdsc.transform(X_test)

我们这里仍然需要注意,StandardScaler在使用过程中只能fit一次

挑选有价值的信息

如果我们发现一个模型在训练集上的效果远优于测试集,那么这就意味着很有可能发生了过拟合,这样的模型收到噪音的影响太大,泛化性不好.可能的原因是使用的模型太过于复杂,常见的解决方案如下:

1. 选取更多的训练数据
2. 使用正则化为过度复杂的情况引入惩罚
3. 选取一个更加简单的模型
4. 减少数据的维数
   接下来的部分我们将介绍如何通过选取特征实现降维和正则化,能给我们带来更加简单的模型

L1和L2正则化作为模型复杂度代价

我们之前提到过一种正则化方法可以实现对模型的简化,通过加上一项L2模
$$L2:||\omega||^2_2=\sum_{j=1}^m\omega_j^2$$
另外一种降低模型复杂度的方法则被称作为L1正则化:
$$L1:||\omega||1=\sum{j=1}^{m}|\omega_j|$$
相较于L2正则化,L1正则化更加适合稀疏的特征(大部分的特征向量中值为0),在这种考虑下,L1正则化可以被看作是一种特征选取的技术

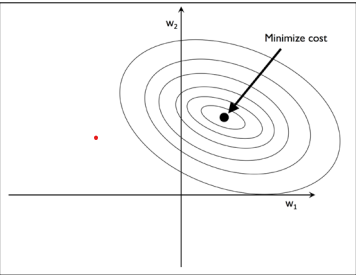
L2正则化的一种几何化解读

正如之前所描述的那样,L2正则化向代价函数中添加了代价项,在研究L1之前,我们先来看看正则化的几何解释

我们首先在$\omega_1$和$\omega_2$两个轴上绘制一个凸函数,在这里,我们将考量方均根误差(SSE),因为这种方法的计算要比使用logistic回归的方式方便很多,但是两者的理念是相同的.,我们需要记住我们要找到的是满足权重较小且误差小的结合,就像在下图中展现的那样

那么,我们可以认为正则化是在尽量的鼓励较小的权重,因此,通过添加正则化参量,我们让最佳点靠近原点

此时$\lambda$可以用来描述这个圆有多重要,倘使$\lambda$非常大,那么这个圆就会变小

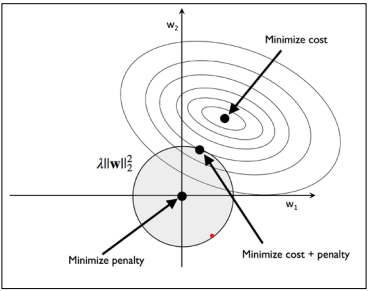
使用L1正则化分散解

现在,我们来讨论L1正则化的结果,虽然有点类似,但是我们需要知道L1正则化是直接绝对值求和,因此可以表示为一个菱形而不是一个圆

在前面那张图中,我们可以注意到代价函数的等高线与L1菱形相交(在$\omega_1=0$处),既然L1正则系统比较尖锐,那么我们可以推断最为理想的状态应当是位于轴上,此时$\omega_1=0$,这就增强了稀疏性
而对于正则化支持L1正则化后的模型,我们可以简单地将penalty参数设定为l1

注意,在这么做时,要将dual设为False,要将solver设为liblinear

1
2

from sklearn.linear_model import LogisticRegression
LogisticRegression(penalty='l1',dual=False,solver='liblinear')

我们将这个方法运用到刚才那个酒类的例子之中,我们可以得到这样的分散解

1
2
3
4

lr=LogisticRegression(penalty='l1',C=1.0,dual=False,solver='liblinear')
lr.fit(X_train_std,y_train)
print('Training accuracy:',lr.score(X_train_std,y_train))
print('Test accuracy:',lr.score(X_test_std,y_test))

Training accuracy: 1.0
Test accuracy: 1.0

可以看到,我们的模型对训练集和测试集都有着完美的描述,接下来我们可以看一看训练的结果参数
其中包含了截距和参数

1
2

print("The w0 is ",lr.intercept_)
print("The wi is",lr.coef_)

The w0 is  [-1.26382301 -1.21599452 -2.36990903]
The wi is [[ 1.24557242  0.18072145  0.74571775 -1.1636765   0.          0.
   1.16100096  0.          0.          0.          0.          0.55564141
   2.50903545]
 [-1.53717924 -0.38698786 -0.99501331  0.36448555 -0.05940712  0.
   0.66768246  0.          0.         -1.93424305  1.23445191  0.
  -2.23163889]
 [ 0.13578242  0.16856474  0.35719175  0.          0.          0.
  -2.43795819  0.          0.          1.56376444 -0.81884123 -0.4924925
   0.        ]]

作为L1正则化的结果,我们可以看到存在一些可能与我们的推断不相关的参数.虽然前面的那个例子可能并不是非常的稀疏,因为里面仍然包含了许多的非零参数,但是我们也可以通过加大C的方式使得正则化强度增加

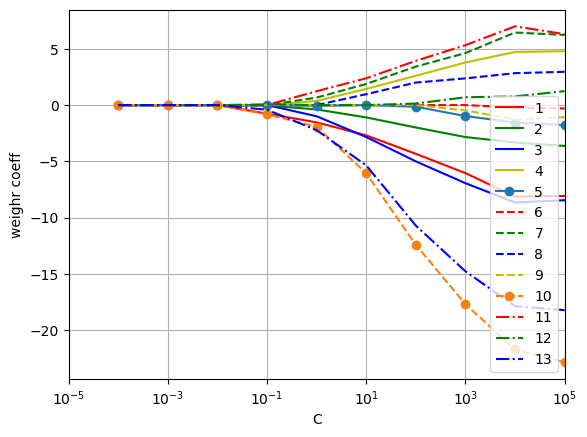
而对于在这一部分的最后一个例子,我们将展现随着C的逐渐增大,正则化参数的效果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

import matplotlib.pyplot as plt
fig=plt.figure()
ax=plt.subplot(111)
def line_gen():  
    """line_gen 产生不超过九个线形

    Yields
    ------
    str
        产生得到线形的字符串
    """    
    line_shapes=["-","--","-.","-*"]
    line_cols=["r","g","b","y","o"]
    for line_shape in line_shapes:
        for line_col in line_cols:
            yield line_col+line_shape

weights,params=[],[]
for c in np.arange(-4.,6.):
    lr=LogisticRegression(penalty='l1',C=10**c,solver='liblinear',random_state=0)
    lr.fit(X_train_std,y_train)
    weights.append(lr.coef_[1])
    params.append(10**c)
weights=np.array(weights)   
lg=line_gen()
for c in range(weights.shape[1]):
    plt.plot(params,weights[:,c],next(lg),label=df.columns[c+1])
plt.xlim([10**(-5),10**5])
plt.ylabel("weighr coeff")
plt.xlabel('C')
plt.xscale("log")
plt.legend(loc='upper left')
ax.legend(loc="best",fancybox=True,ncol=1)
ax.grid(True,'both')
plt.show()

​

​

我们可以看到如果我们将C设置很小(相当于很高的正则化参数),那么各个参数将会趋向0

序列特征选择算法

另外一种降低模型复杂度并且避免过拟合的手段是降维法,常见有两种降维的手段:特征选取和特征提取,使用前者我们会得到特征的一个子集,使用后者我们则会得到一个全新的特征空间

在这一部分中,我们将讨论一个特征选择算法中传统的一族.

序列特征选择算法是一种贪心算法,其目的在于选取出与与问题关联程度最高的子集,可以提高计算效率并且降低误差的影响

一个经典的序列特征选择算法是序列后向选择(SBS),其目的在于减少初始特征子空间位数,而SBS在模型面临过拟合的困境时,还可以提高模型的说服力.

SBS算法背后的思想非常简单,SBS一步步减少特征直到最后拥有指定数量,而为了判断移除特征的顺序,我们需要定义一个标准函数$J$达到最小值,这个函数可以简单地认为是保留这个特征和删除这个特征训练效果之差,也就是说让这个函数最小的特征可以被看作是最不重要的特征

虽然书中原文讲并没有可以实现这个目的的函数,但是可能由于版本迭代,我在这里看到了有关函数的资料,也许可以用一下

1
2
3
4
5
6
7
8
9
10
11
12

from sklearn.feature_selection import SequentialFeatureSelector
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
scorel=[]
for i in range(1,13):
    sbs=SequentialFeatureSelector(KNeighborsClassifier(p=2),n_features_to_select=i,direction="backward")
    sbs.fit(X_train_std,y_train)
    nxt=X_train_std[:,sbs.support_]
    c=KNeighborsClassifier(p=2)
    c.fit(nxt,y_train)
    sc=accuracy_score(c.predict(nxt),y_train)
    scorel.append(sc)

在上面,我们应用了所给的SequentialFeatureSelector进行后向选取,但是我们需要注意到,在我们对分数进行评估的时候,必须要使用训练集进行评估,实际上是要保证测试集的数据无论如何不会影响到训练过程,否则测试集的效果将会降低

下面展现出使用序列选取后准确率的效果

1
2
3
4
5

plt.plot(list(range(1,13)),scorel,"*-")
plt.xlabel("Number of features")
plt.ylabel("Accuracy")
plt.grid(True,"both")
plt.show()

​

​

其他还有许多类型的选取方法,可以去参考官方网页

使用随机森林方法评估特征的重要性

在之前的部分中,我们通过L1正则化方法学会如何去除无关的特征,另外一种常用方法是随机森林,因为在之前我们就提到过,随机森林会随机选取某些特征和某些样本进行训练,在我们训练完后,我们就可以得到不同特征的重要程度

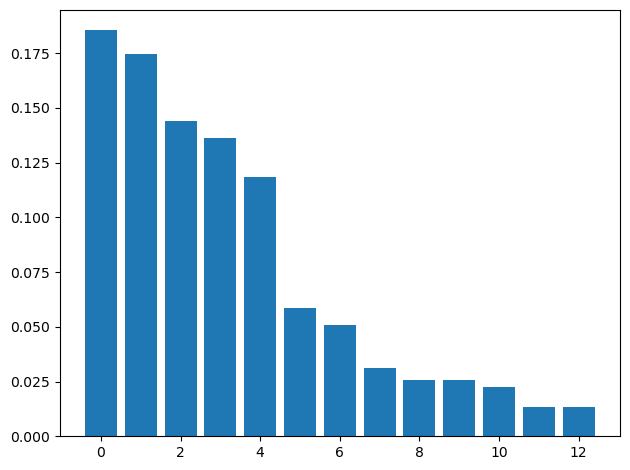
1
2
3
4
5
6
7
8
9

from sklearn.ensemble import RandomForestClassifier
flabel=df.columns[1:]
forest=RandomForestClassifier(n_estimators=500,random_state=1)
forest.fit(X_train,y_train)
imp=forest.feature_importances_
indices=np.argsort(imp)[::-1]
plt.bar(range(X_train.shape[1]),imp[indices],align='center')
plt.tight_layout()
plt.show()

​

​

从这张图我们可以清晰地看出哪些特征更加重要

作为对随机森林的总结,sklearn里面还包含了一种SelectFromModel类支持用户用自定义阈值来实现模型选取,那么我们就可以用随机森林作为中间步骤,例如我们下面就可以将阈值设为0.1,看到五个最为重要的特征

1
2
3
4

from sklearn.feature_selection import SelectFromModel
sfm=SelectFromModel(forest,threshold=0.1,prefit=True)
X_selected=sfm.transform(X_train)
X_selected

总结

我们首先看了处理缺失数据的正确方法,然后对数据进行编码以方便进行学习

接下来,我们介绍了L1正则化方法,可以规避过拟合现象发生,同时,选取合适的学习特征也有其他的手段可以使用.