以下内容主要包含光学期末复习相关笔记
内容整理
光的干涉
光干涉的几个要求
频率相同,振动方向相同(可能这里指的是分量),相位稳定
干涉光强计算
$I=\frac{1}{2}EE^*$,对于相干光,是$E$的叠加;对于非相干光,是$I$的叠加
频谱宽度的计算与注意事项
$\Delta x\Delta k\approx 2\pi$其中$\Delta x$为发光长度
或者可以用
$\Delta t\Delta \nu=1$,其中$\Delta t$为发光时间
相干光的两种产生方式
分波前与分振幅
典型分波前干涉:杨氏双缝干涉
$$I=I_0\cos^2\left(\pi\frac{\Delta xl}{L\lambda}\right)$$
需要注意,这里假定缝非常小,否则还要考虑光的衍射
杨氏双缝干涉中单缝作用
用来产生相干光
随着与中心距离的逐渐变大,条纹会逐渐变暗,一般有两个原因:
- 干涉距离变大,逐渐变得不相干
- 由于后面会讨论的衍射因子的作用
如果非单色光,那么会出现分光的现象
分波面干涉:劈尖干涉与牛顿环
需要注意,在分拨面干涉中的光路并不是任意的,需要注意成像问题
对于劈尖,需要关心介质的折射率关系以分析半波损失
关于牛顿环,可以直接计算透镜的曲率半径$R$为
$$R=\frac{r^2_{m+i}-r^2_m}{i\lambda}$$
等厚干涉与等倾干涉的综合区别
等厚干涉的光程差来源于不同位置透明介质厚度不同,等倾干涉光程差来源于不同位置光角度不同,经过厚度不同
迈克耳孙干涉
需要注意到的问题:
- 在第一个反射镜处,是否有镀膜会对干涉的半波损失带来巨大影响
- 如果没有补偿镜,需要使用单色性更好的光
多光束干涉
相当于在薄膜干涉的基础上多考虑反射和折射
可以得到总的反射相对光强和总的投射相对光强
$$\frac{I_r}{I_i}=\frac{F\sin^2(\frac{\sigma}{2})}{1+F\sin^2(\frac{\sigma}{2})}$$
$$\frac{I_t}{I_i}=\frac{1}{1+F\sin^2(\frac{\sigma}{2})}$$
此处$\sigma=\frac{4\pi n h \cos\theta_t}{\lambda}$为每一级条纹之间的相位差($\theta_t$为介质中投射角),$F$为锐度系数$F=\left(\frac{2r}{1-r^2}\right)^2$
同时,我们可以定义从光强最大到光强为$\frac{1}{2}$的距离为半峰宽$\delta_{\frac{1}{2}}$,可以有
$$\delta\theta\frac{4\pi nh\sin\theta_t}{\lambda}=\delta_{1}{2}=2\arcsin(\frac{1}{\sqrt{F}})\approx\frac{2}{\sqrt{F}}$$
从这里,我们可以求解出来其角分辨能力
衍射理论
近场与远场
远场:满足射入的光近似于平行光(或者用透镜实现无穷远成像)菲涅尔衍射
近场:存在角度夫琅和费衍射
单个狭缝的夫琅和费衍射
分析手段
- 可以使用矢量图法,每一小部分光源相当于构成了一个小矢量,而这些矢量首尾叠加构成圆弧,合成光就是圆弧首尾相连
- 可以使用半波带法分析明暗条纹
- 直接积分
结果
记住光强为
$$I=\frac{\sin^2\beta}{\beta^2}$$
其中$\beta=\frac{\pi b}{\lambda}\sin\theta$(可以看作以某一角度射出时极限光程差相位差的一半)
特殊情况
如果入射光存在角度,那么需要叠加计算
$$\beta=\frac{\pi b}{\lambda}(\sin\theta+\sin\alpha)$$
其中$\alpha$新入射效果
矩形孔
可以看作两个方向的狭缝,最后结果就是两个方向衍射相乘
圆孔夫琅和费衍射
我们无法获得圆孔夫琅和费衍射的解析解,其可以被写作$U(\theta)=\frac{2kJ_1(x)}{x}$
而$\frac{2\pi}{\lambda}a\sin\theta$,$a$为圆孔半径
因此,可以得到第一个暗环的半角宽为$\delta\theta=0.61\frac{\lambda}{a}=1.22\frac{\lambda}{D}$
这也是最小角分辨率,而对于研究线分辨率$d=\Delta\theta f$
多缝衍射
对于多峰衍射,可以考虑干涉因子和衍射因子相乘
其中干涉因子与一个完整的遮挡和缝的总宽度$d$相关
$$I=I_0\frac{\sin^2N\gamma}{\sin^2\gamma}\frac{\sin^2\beta}{\beta^2}$$
其中干涉的强度极大值位置为$d\sin\theta=\pm m\lambda$,极小值$\sin N\gamma=0$且$\sin\gamma\neq 0$
注意,如果$d$和$b$呈现简单整数比,那么会存在缺级
角色散率
我们可以定义角色散率$D=\frac{\delta\theta}{\delta\lambda}$
可以得到:级次越大,角色散率越大,刻线越密,色散越大
而使用瑞利判据,可以得到色分辨本领$R=\frac{\lambda}{\Delta\lambda}=mN$
$N$为总刻线数
闪耀光栅
我们可以让反射面倾斜,这样可以使得衍射极大发生偏离,使得干涉级数大的部分比较亮
菲涅尔衍射
分析:可以使用半波带法,如果有奇数个半波带,那么光强较强,偶数个半波带,光强较弱
三种不同的情况
- 光阑,随着$r$变大,会从一个亮点中间产生黑点再生长….
- 自由传播:总光场一半
- Posson亮斑:中心点总是亮的
光阑的半波带个数
在光阑半径为$R$一点与光阑中心的那一点的光程差
$$\Delta S=\frac{R(r_0+\rho)}{\rho r_0\lambda}$$
$\rho$为波面半径,$r_0$为波面到观测点的最短距离
可以利用半波带性质做透镜,满足
$$(\frac{1}{\rho}+\frac{1}{r})=\frac{m\lambda}{R^2_m}$$
几何光学
几何光学成像
物空间->光学系统->像空间
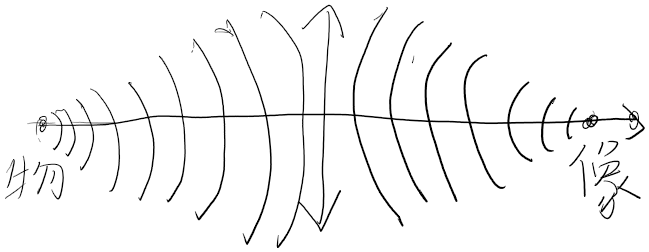
理想透镜
原理光程相等,构成波阵面,一般理想透镜的透镜方程
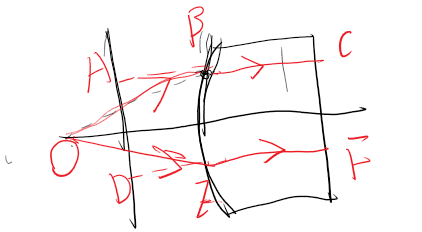
对于双曲面镜,有AD为双曲面准线,O为双曲线一个焦点,如果$e=\frac{n}{n_0}$
那么可以知道OB光程加上BC光程相当于在玻璃介质中AC,因此双曲面镜可以点源到平行光
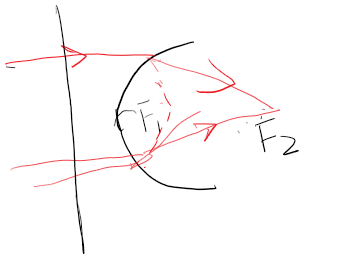
相似的,椭圆面镜也可以使平行光汇聚
如何判断应当使用双曲面镜还是使用椭圆面镜的手段
在双曲面镜中,平行光出现在折射率大的部分
在椭圆面镜中,平行光出现在折射率小的部分
可以使用双曲面+球面(光线过球心,不会在表面折射)制作理想双曲面镜
球面透镜
对于球面透镜,我们往往需要进行小角度近似,可以得到
$$\frac{n_1}{s_o}+\frac{n_2}{s_i}=\frac{n_2-n_1}{R}$$
实虚关系
成像符号约定
| 类型 | 符号 | 类型 | 符号 |
|---|---|---|---|
| 实物$s_o$>0 | + | 虚物$s_o$<0 | - |
| 实像$s_i>0$ | + | 虚像$s_i<0$ | - |
| 球心在球面右侧 | + | 球心在球面左侧 | - |
薄透镜
设外界折射率为$n_m$,透镜折射率为$n_l$,则有透镜成像公式
$$\frac{1}{s_o}+\frac{1}{s_i}=\frac{1}{f}=\frac{n_l-n_m}{n_m}\left(\frac{1}{R_1}-\frac{1}{R_2}\right)$$
需要注意,焦距的决定式很重要,需要专门记忆(注意分子上的$n_l-n_m$)
对于$R_1,R_2$的符号,参考上表
作图法求解光学问题
对于单次成像的问题,往往使用三条光线
- 过光心
- 过第一个焦点
- 平行于光轴
但是有时会要有多个透镜多次成像,此时可以先绘制出一个透镜的成像,然后做出从该像过第二个透镜光心的光线
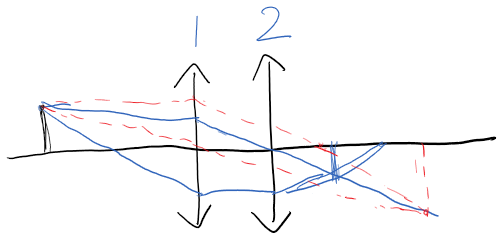
例如此处红色光线就是透镜1所成的像(在实际中不会被看到),转换成蓝色线所成的两次叠加成像.
光阑
入射光瞳:从物的位置看到的孔的像
出射光瞳:从像的位置看到的孔的像
曲面镜
抛物面镜:将平行光汇聚在焦点(有时常常会用离轴抛物面镜)
共轭点成像:对于椭圆面镜或双曲面镜,一个焦点和另一个焦点
球面镜:可以类比于透镜成像,但是有关符号,需要注意
球面镜的等效焦距为$-\frac{R}{2}$,但是此时像距的符号与位置和实虚关系是反的,同时,对于凹面镜成像,$R$是负的,因此$f$是正的,从而有可能成实像.
棱镜
偏向角$\delta=\theta_{i1}+\theta_{t2}-\alpha$
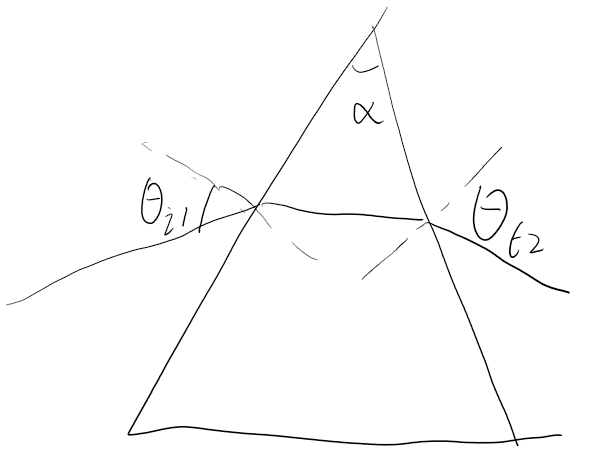
关于$\delta$,满足有
$$\delta=\theta_{i1}+\arcsin (\sin\alpha(n^2-\sin^2\theta_{i1})^\frac{1}{2}-\sin\theta_{i1}\cos\alpha)-\alpha$$
需要注意的是,当**$\theta_{i1}=\theta_{t2}$时,有偏向角最小**
如果要使用棱镜做光谱,需要使用透镜制造平行光
人眼
不考虑任何病变,人眼最为理想的成像状态是平行光入射
这个平行光入射在设计制造光学仪器的过程中非常重要
眼镜可以被看作紧贴于眼睛的一个透镜,可以直接焦距合成
$$\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}$$
或者是定义屈光度为$\mathcal{D}=\mathcal{D_1}+\mathcal{D_2}$
一般而言$1D$的屈光度意味着透镜焦距为1m
眼镜的作用
近视眼镜将无穷远点投射到近视眼的远点上,远视眼镜将正常人的近点投射到远视眼的近点上
色差
因为一块玻璃对于不同波长的光的折射率存在区别,因此不同波长的光在透镜中会发生色散
而根据前面提到的透镜焦距公式
$$\frac{1}{f}=\frac{n-n_0}{n_0}(\frac{1}{R_1}-\frac{1}{R_2})$$
我们能够计算出不同颜色光波长的色差
而使用一块凹透镜和一块凸透镜可以较好地消除色差
光的偏振
一般而言,光矢量都可以被分解为$x$,$y$两个分量,对于自然光而言,光的偏振是杂乱无章的
产生偏振光的方法:
利用二项色性:可以使只有某一个方向的偏振光通过,于其正交的偏振光被吸收
满足马吕斯定律$I=I_0\cos^2\alpha$
利用反射:非偏振光在反射后也会成为良好的偏振光
双折射现象
首先是光轴,一般而言,我们讨论的问题中只有一个光轴,可以有以下的简单结论
沿光轴的相对介电常数和垂直于光轴的相对介电常数不同
于是,我们就可以分出来寻常光(o光)和非常光(e光)
寻常光与光轴平行的光,偏振方向垂直于光轴,因此传播不受到影响
非常光与光轴垂直的光,偏振方向存在垂直光轴和平行光轴的成分,因此传播会受到影响
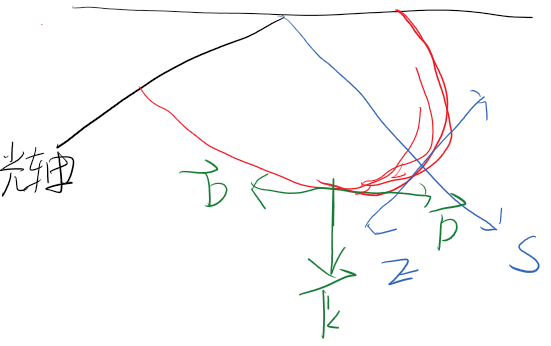
如图所示的波阵面图像,可以看到原本光的波矢是竖直向下的
需要注意到,即使是e光,其电位移矢量与波矢的方向(绿色线)保持不变,但是像电场强度与坡印廷矢量的方向(蓝色线)发生偏移
为什么波矢方向不变,我们仍然认为e光传播方向发生了变化原因在于
我们看到所谓光线,是由于光的直线传播,而从光的波动推导到直线传播是通过计算光的干涉得到相干相长的结论实现的
而光的干涉则是光电场相互叠加的结果,并且$S$传递能量(这只是个人猜想)
双折射的惠更斯做图
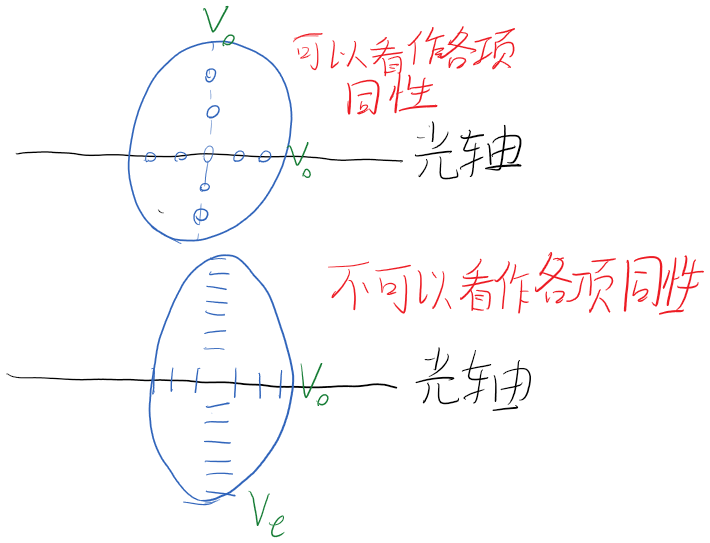
可以看出,当偏振方向与光轴垂直的波速为$v_o$,对应的折射率为$n_o$
当偏振方向与光轴平行的波速为$v_e$,对应的折射率为$n_e$
$n_o<n_e$为正晶体
$n_o>n_e$为负晶体
可以使用这个图像来确定光的传播
波片的使用
波片的使用可以让两个方向的偏振光发生一个相位变化,导致可能出现干涉
克尔效应与泡克耳斯效应
透明介质放在电场中会出现双折射现象$n_e-n_o=\lambda_0 KE^2$
同时可以利用这一效应做克尔盒对相位进行调节$\Delta\varphi=2\pi KlV^2/d^2$($l$为盒子的长度)
而泡克耳斯效应的相位差则为$\Delta\varphi=2\pi n_0^3r_{63}V/\lambda_0$
综合性内容
“恰好分辨”
对于波长存在范围的干涉而言,恰好分辨是前一级条纹中波长最大和后一级条纹波长最小重合
相似的,在杨氏双缝干涉实验中,如果光源有限宽,可以考虑一个端点到另一个端点的0级和1级条纹重合
对于多光束干涉而言,恰好分辨是两个干涉峰恰好错开半峰宽(这可以认为是一种较为简单的判据)
对于多光束干涉使用瑞利判据,一般认为两光束合成后亮度的鞍点亮度为最大辐照亮度的$\frac{8}{\pi^2}$倍,这个时候的推导要更为复杂,但是可以直接记住结论:使用该判据,两个光束的衍射相位差至少为
$$(\Delta\delta\approx\frac{4.2}{\sqrt{F}})$$
对于衍射的瑞利判据,恰好分辨是一个衍射极大恰好落在另一个衍射极小
相矢量图
这个问题主要来自于多缝衍射
首先,多缝衍射倘使不考虑缺级以及如衍射光强等一系列问题,完全可以看作多缝干涉的模型,此时我们可以通过绘制相矢量图来解题
但是这个时候,需要关注到一个易错点:相矢量图两个矢量之间的夹角就是光程差带来的相位差,但是在式子$\frac{\sin^2(N\alpha)}{\sin^2\alpha}$中$\alpha$的定义确是前者的一半
同时,我们需要知道辅极大的位置无法直接求解,近似在$\sin N\alpha$取极大的位置上
而对于极小的位置,就是$\sin N\alpha=0$的位置(这在求解恰好分辨的问题非常重要)
人眼的分辨能力与仪器放大率
放大率的种类
横向放大率$M_T=\frac{y_i}{y_o}–\frac{v}{u}$
纵向放大率$M_L=\frac{dv}{du}$(这个代表像会拉的多长)
纵向放大率的选取:对于一般照相机,希望能同时拍摄到近处景物和远处景物,那么此时$M_L$要尽量小
但是对于一些其他的成像设备(例如显微镜),需要让成像的平面性尽量强,那么就要选择大的$M_L$
角放大倍率$M=\frac{\theta’}{\theta}$
其中,$\theta$为人眼在明视距离的条件下看这个物体的张角
放大镜与目镜
一般而言,放大镜的角放大倍率前面已经说明
但是需要注意到的是,如果物体放在放大镜的焦平面上,那么此时放大镜出来的是平行光(最理想状态)
此时的角放大率$M=\frac{25cm}{f}$
显微镜与望远镜
显微镜和望远镜可以看做一个物镜加一个目镜实现,其中最后的放大率为$M=M_{To}M’$为物镜的横向放大率乘以目镜在该成像条件的角放大率
而一般而言,从目镜中出来的应当是平行光
那么此时从显微镜出来的放大率$MP=(-\frac{160mm}{f_o})(\frac{254mm}{f_e})$(160mm为标准目镜和物镜焦距距离)
而从望远镜出来的放大率$MP=-\frac{f_o}{f_e}$(默认入射光为平行光)
数值孔径,$f$数与衍射
数值孔径可以理解为介质折射率乘以收光的半角度正弦$NA=n\sin\theta\approx\frac{nD}{2f}$后面一个近似是在$f$很大的时候成立
而在一些相机镜头中,会定义焦比(f数)$f/#=\frac{f}{D}$
这样的定义是用在研究夫琅禾费衍射所产生的光斑,光斑的半径$1.22f\frac{\lambda_n}{D}$
数值孔径越大,其理论分辨极限越大,提高数值孔径有三种方法:
- 增大镜头直径
- 降低焦距
- 提高折射率(例如使用油镜)
同时,我们也需要注意到,数值孔径会影响横向放大率
有时题目会给出数值孔径与瞳孔直径,然后要求正常放大率,可以这样考虑
- 从数值孔径可以得到最小分辨长度$s=0.61\frac{\lambda}{NA}$
- 可以使用人眼明视距离得到人眼最小分辨长度$s’=1.22\frac{s_0\lambda}{D}$
- 放大率要相互匹配.即$sM=s’$
做题存在问题
在每一次做到和干涉衍射相关的题目时,需要小心的分析半波损失问题
需要去理解半波带法的绘图
多看闪耀光栅的题目
如果两个发光点相距很远,那么在整个空间中,可以看作总体的$I_1I_2$的空间平均为0,如果两个发光点距离很近(远小于一个波长),可以看作一个光源,亮度为两倍
波片与旋光性的区分:
波片的讨论往往使用的是分解为两个线偏振光
旋光性的讨论往往使用的是分解为左旋光和右旋光
两个同样厚度,但是摆放方向呈现镜像关系的会让o光和e光又回到一起
焦深可以认为是成像移动前后多少还能近似看清的一个量度
共轭光线指物空间和像空间互相对应的点
虽然PPT中没有涉及到关于光阑的问题,但是近似记住:成像系统的入射光瞳就是物镜的直径,出射光瞳往往是物镜通过目镜成的
虽然没有说考,但是在使用偏振的时候还是可能会涉及到
关于双折射定律中,倘使光轴在光学平面内,那么可以用以下公式计算折射率(其中$\theta$为法向和光轴方向夹角)
$$n^2(\theta)=\frac{n_o^2n_e^2}{n_e^2\cos^2\theta+n_o^2\sin^2\theta}$$
对于偏振器件要加以了解,例如尼科尔棱镜
在瑞利斑相关计算中,对于从直径求角度变化使用的系数都是1.22,使用0.61只有在使用孔半径或者使用数值孔径时才会出现
在考虑多缝衍射模型,注意零点光强不是1
关于反射光栅,应当更加仔细去分析光路,因为可能有倍数关系
注意观察是要求艾里斑的半径还是直径
计算薄膜干涉时,不要忘记折射率
在做几何光学题目时,记得符号
放大率的符号包含了正倒关系
注意如果有反射的问题小心光程是否需要乘2
注意:**半峰宽$\gamma$是两倍的$\delta_{\frac{1}{2}}$
看到要立刻想起来的公式
$k,E,B$依次构成右手坐标
玻印亭矢量定义$S=\frac{1}{\mu_0}E\times B$
偏振光的反射与折射强度
对于$E$平行于光线所在平面的例子
$$r=\frac{n_t\cos\theta_i-n_i\cos\theta_t}{n_i\cos\theta_t+n_t\cos\theta_i}$$
$$t=\frac{2n_i\cos\theta_i}{n_i\cos\theta_t+n_t\cos\theta_i}$$
对于$E$垂直于光线所在平面的例子
$$r=\frac{n_i\cos\theta_t-n_t\cos\theta_t}{n_i\cos\theta_i+n_t\cos\theta_t}$$
$$t=\frac{2n_i\cos\theta_i}{n_i\cos\theta_i+n_t\cos\theta_t}$$
(从中可以得到布儒斯特角)
频谱宽度计算$\Delta t\Delta v=1$
多光线干涉
相位差$\sigma=\frac{4\pi nh\cos\theta_i}{\lambda}$
锐度系数$F=(\frac{2r}{1-r^2})^2$
从最大光强到光强一半的距离为半峰宽$\delta_{\frac{1}{2}}=2\arcsin(\frac{1}{\sqrt{F}})\approx\frac{2}{\sqrt{F}}$
(判断两个条纹是否可以分辨就是看两个条纹间距恰为一个半峰宽)
偏振仪器:
克尔盒:$\Delta\varphi=2\pi KlV^2/d^2$
跑科尔斯效应$\Delta\varphi=2\pi n_0^3r_{63}V/\lambda_0$
几何光学:
透镜焦距公式$\frac{1}{f}=\frac{n-n_0}{n_0}(\frac{1}{R_1}-\frac{1}{R_2})$
显微镜角放大率$MP=(-\frac{160mm}{f_o})(\frac{254mm}{f_e})$
数值孔径$NA=n\sin\theta$
在计算衍射与多光束干涉,要记得光程差除以二再代入式中
瑞利斑的半径为$1.22f\frac{\lambda_n}{D}$
光阑半径R处一点到中心光程差(用于计算菲涅尔衍射)$\Delta S=\frac{R(r_0+\rho)}{\rho r_0\lambda}$
尼科尔棱镜e光穿透,o光保留(依靠折射率不同出现双折射)
格兰-汤普森棱镜不依靠双折射
罗尚棱镜依靠光轴方向旋转分光(这些棱镜大多使用负晶体)
角色散率$D=\frac{\delta \theta}{\delta\lambda}$
基尔霍夫衍射$$U(P)=K\int U_0(Q)\frac{1}{2}(1+\cos\theta)\frac{e^{ikr}}{r}d\Sigma$$