以下内容主要包含复变函数的相关笔记(基本定义到微分和积分)
复数
基本定义(直角坐标定义)
对于一个复数$z=x+iy$,其实部为$\Re[z]=x$,其虚部为$\Im[z]=y$
极坐标定义
由于前面的定义,我们可以看到一个复数可以对应于在坐标上的一个点(或者是一个矢量),那么既然有一个直角坐标定义,那么肯定会有一个极坐标定义
$z=\rho e^{i\theta}$,其中模长$|z|=\rho$,辐角$Arg z=\theta+2k\pi$
这里我们需要注意到,对于一个复数,其辐角不是唯一的,一般而言,我们为了方便起见,对于一个复数,我们可以选取$[0,2\pi)$的一个辐角作为其主辐角
但是我们仍然需要注意到在一些函数中,辐角的多值性会导致函数的多值性
两个特殊点
两个特殊点:零点与无穷远点
其中可以用一种方式联系起来:假设一个球与复平面相切,可以使用映射用切线实现,此时,底部的点相当于零点,顶部的点相当于无穷远点
运算
加减运算,可以看作矢量加减法,其中也可以推导出相关的不等式性质
$$|z_1+z_2|\le|z_1|+|z_2|\|z_1-z_2|\ge|z_1|-|z_2|$$
复数的积$z_1z_2=(x_1x_2-y_1y_2)+i(x_1y_2+x_2y_1)=\rho_1\rho_2e^{i(\varphi_1+\varphi_2)}$
复数的商$\frac{z_1}{z_2}=\frac{x_1x_2+y_1y_2}{x_1^2+x_2^2}+i\frac{x_2y_1-x_1y_2}{x_1^2+x_2^2}=\frac{\rho_1}{\rho_2}e^{i(\varphi_1-\varphi_2)}$
可以看到,这里的复数的积和商使用极坐标方法更加方便
开方$\sqrt[n]{z}=\sqrt[n]{\rho}e^{i\frac{\varphi}{n}}$
注意到,这里对于一个复数$z$,那么$\frac{2k\pi}{n}(k<n)$,的辐角变化后这仍然是函数的结果,这就导致了函数的多值性
复变函数
对于复变函数定义
$\omega=f(z)$代表着从一个复平面上的点集到另外一个复平面的点集
对复平面上的一个点集$E$中每一个点$z$,按照规则存在一个/多个复数值$\omega$与$z$对应,此即为复变函数
区域
为了方便起见,我们往往会将讨论的范围限制在区域上的函数
为了定义区域,我们需要定义以下内容:
- 内点:若$z_0$及存在邻域均属于$E$,则为内点
- 外点:若$z_0$及存在邻域均不属于$E$,则为外点
- 边界点:若$z_0$及所有领域均存在属于$E$和不属于$E$,则为边界点
区域的定义:满足以下两个条件的点集,被称作为区域:
- 全部由内点构成
- 具有连通性
如果是区域加上边界线,那么可以表示为闭区域
常见的复变函数
- $e^z=e^x(\cos y+i\sin y)$
- $\sin z=\frac{1}{2i}(e^{iz}-e^{-iz})$$\sinh z=\frac{1}{2}(e^z-e^{-z})$
- $\cos z=\frac{1}{2i}(e^{iz}+e^{-iz})$$\cosh z=\frac{1}{2}(e^z+e^{-z})$
- $\ln z=ln|z|+iArg z$(注意,不唯一,且有无穷多值)
一般而言,一个复变函数可以表示为$f(z)=u(x,y)+iv(x,y)$(变为一对二元实变函数)
复变函数求导与解析函数
复变函数可导的两个条件
- $\omega=f(z)$为单值函数
- 极限$$\lim_{\delta z\to 0}\frac{f(z+\delta z)-f(z)}{\delta z}$$存在且与$\delta z\to 0$方式无关
复变函数可导的柯西-黎曼条件
考虑沿实轴逼近和沿虚轴逼近:
沿实轴逼近:
$$\frac{\partial f}{\partial z}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial z}=\frac{\partial u}{\partial x}+i\frac{\partial v}{\partial x}$$
沿虚轴逼近
$$\frac{\partial f}{\partial z}=\frac{\partial f}{\partial y}\frac{\partial y}{\partial z}=\frac{\partial v}{\partial y}-i\frac{\partial u}{\partial y}$$
需要保证两者相等,因此有:
$$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}\\frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}$$
此即为柯西-黎曼条件(C-R条件)
在推导的过程需要注意虽然假定了沿实轴(虚轴)逼近,但是从$\frac{\partial f}{\partial z}$到$\frac{\partial f}{\partial x}$中间还有要考虑$\frac{\partial z}{\partial x}$
复变函数可导的充分条件
在满足C-R条件的基础上,如果同时满足$u,v$的偏导数连续,那么必然可导
解析函数
若$f_0$在$z_0$及其邻域$E(z_0)$处处可导,那么称$f(z)$在$z_0$处是解析的
(如果在区域中处处可导,那么其处处解析)
解析函数需要满足的性质
$f(x,y)=u(x,y)+iv(x,y)$
其中$u,v$需要是调和函数,即$\nabla^2u=\nabla^2v=0$
同时有$\frac{\partial f}{\partial z^*}=0$
这个性质的证明和应用都用到了对所有复数$z=x+iy$,都有$x=\frac{z+z^*}{2}$,$y=\frac{z-z^*}{2}$
因此,解析函数对$z^*$偏导恒等于0意味着解析函数必然可以被写作$u(z)+iv(z)$的形式
多值函数
在这里,我们将以一个例子开始,分析多值函数的性质
设$w=\sqrt{z}$,可以将$w$的模长和辐角提取出来,我们得到
$$r=\sqrt{|z|},\theta=\frac{1}{2}Argz=\frac{1}{2}argz+n\pi$$
那么我们注意到,$w$的主辐角可以取$\theta_1=\frac{1}{2}argz,\theta_2=\frac{1}{2}argz+\pi$
这里给出了两个不同的值
可以看作为两个单支
我们要注意到,这和实函数中的多值函数不同,这里的多值不独立
支点
对于给定多值函数$w=f(z)$,$z$绕某点一周,$w$不复原,那么该点为多值函数的支点
例如,对于前面的那个例子
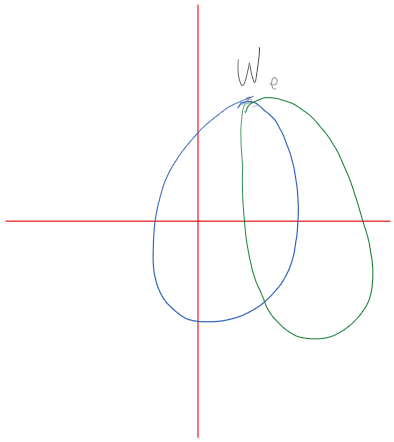
可以注意到若$w$沿蓝色线转一圈,那么会跑到另外一支上,但是如果沿着绿色线转一圈,就不会,因此可以说$z=0$是函数$\sqrt{z}$的支点
同时,如果绕着该点转$n$圈可以回到原来的函数值,那么称该点为函数的$n-1$阶支点
比如$z=0$就是一阶支点
黎曼面
我们从刚才这个例子可以看出总共可能会有两支,但是这种展示方法并不直观
我们可以通过建立两张复平面实现将辐角从$2\pi$到$4\pi$,如图所示,将BC相连,DA相连
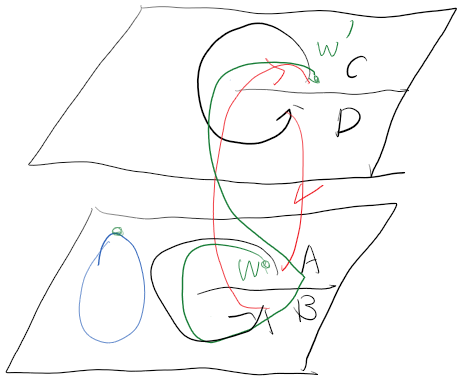
那么前面绕支点转一圈的例子就非常明显了(绿线),其不能像蓝线那样回到原处