之前提到过三维路径的查找的方法,使用A*寻找,但是在找完之后就面临一个问题,如何挑选出一个合适的路径.
很明显,我们这里的这个问题是一个旅行商问题,这玩意不可能有一个”完美”的算法.
之前我所使用的方法是使用基于贪心算法的最小生成树进行路径查找但是这种方法的结果只能保证路径总代价不超过2倍.
原本我想想只需要无脑调库就可以了,但是一查,虽然有一个民间制作的蚁群优化算法,但是那些都是基于python的python库,完全没法用.
虽然你可能会觉得上面那句话很怪,但如果你了解过python的运行效率,那么就会知道这么做就是自寻死路
所以我看来又得”自己造轮子”,使用C++处理蚁群算法
蚁群算法机理
这里的机理我主要参考的这篇知乎文章,在这里我简单介绍以下(当然也包括我的一些实现细节,便于未来查找错误)
基本原理
蚁群算法的基本处理方式是在原本的类似于贪心算法(但又不完全贪心)上添加了一个信息素矩阵,并且选取的途径并不是”决定性”的选取,而是概率选取,越符合要求的选取到的概率越高.
同时这个信息素的产生和变化遵循以下条件:
- 不同蚂蚁产生信息素相互线性叠加
- 一只蚂蚁在所有路径上分泌的信息素总和为定值
- 信息素在每次迭代后都会挥发一部分
使用这种方法实现结果
具体实现
首先是概率的计算,在每一只蚂蚁选择下一个点(从$i$到$j$)时,每一个点的概率为
$$p_{ij}=\frac{t_{ij}^\alpha r_{ij}^{\beta}}{\sum_j t_{ij}^\alpha r_{ij}^{\beta}}$$
其中$t_{ij}$为从$i$到$j$的信息素含量,而$r_{ij}$则为基于贪心的路径选择$r_{ij}=\frac{1}{L_{ij}},L_{ij}$为这两点之间的距离,具体如何通过$p_{ij}$来进行选取,我们采用的是”轮盘赌”的方法,可以参考这篇文章
而每次迭代之后,对于$t_{ij}$其变化为
$$t_{ij}=pt_{ij}+\sum \frac{G}{L_i}$$
其中,$p$为挥发后剩余量,$G$为常数,$L_i$为经过这个边的第$i$个个体总路径长度.
而在达到迭代次数后,输出计算得到的结果.
关于$G$的选取和初始化
我们面临一个初始化的问题,就是在第一次迭代之前,如何选取$t_{ij}$,我目前的做法是将其全部初始化为1,而令$G=n\bar{L_{ij}}$,即边长平均值乘以$n$,(类似于平均边长)
代码结构
目前我的C++程序库使用的结构定义了一个MapSearcher类,其构造函数确定各个点间的连接矩阵road_mat,每个点的蚂蚁数ant_num_per_point,保留率p,以及$\alpha,\beta$,同时,为了保证结果的可重复性,其可以指定随机数种子.
在初始化后,one_iter方法迭代一次,并且返回最佳结果的总长度
类中有三个只读属性best_now保存目前全局最佳结果总长度,best_route返回这一结果所对应的路径(以list形式返回),tmat保存系统目前的信息素矩阵
目前效果
下面展示了50个随机点$\alpha=2$,$\beta=1$的计算处理的收敛图像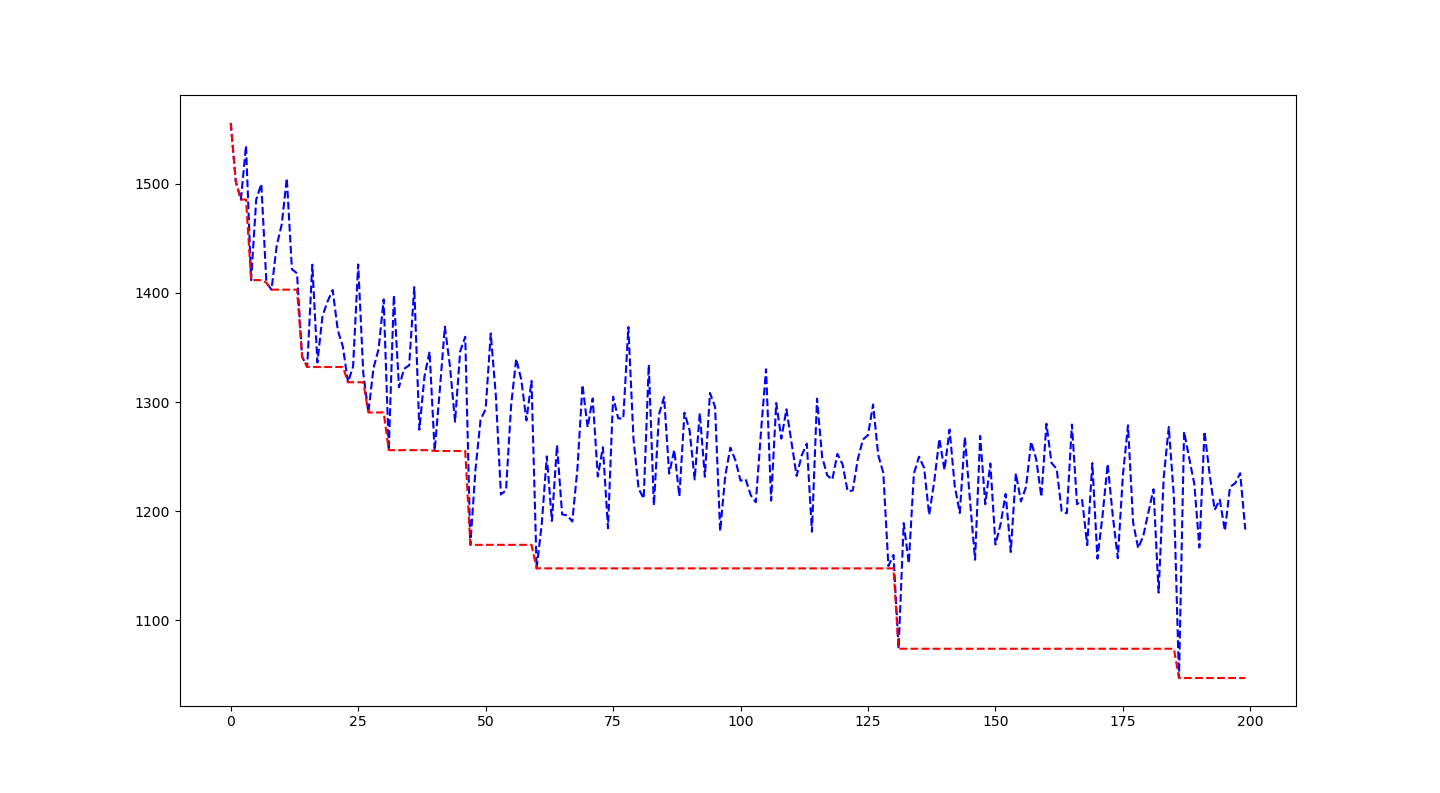
可以看出来200次迭代有较好的收敛能力.
但是我们为了更好研究结果与实际的最小相差多少,我们采用网格点进行测试
我们在网格上按照正方形排布均匀放49个点,然后经过迭代,得到了以下结果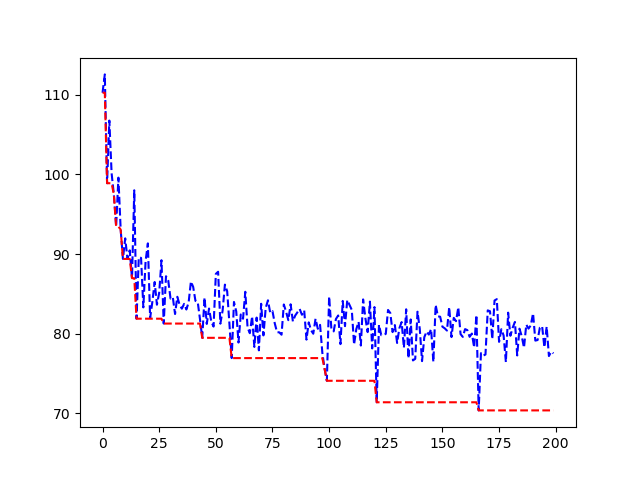
其路径为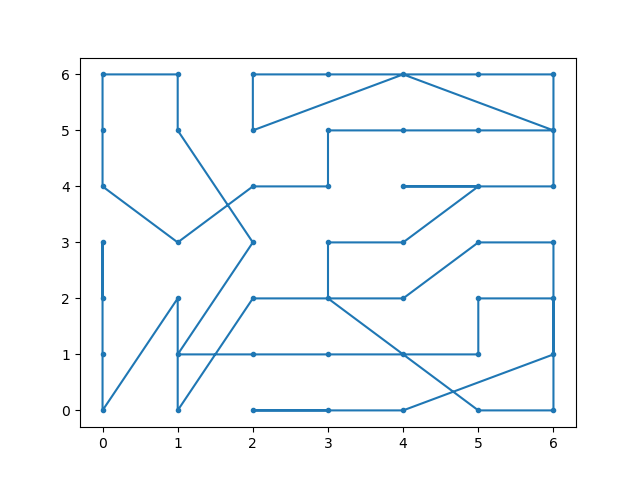
可以看出来,其实这种方法得到的结果与理论极限48有着较为明显的差距,还需要进一步优化
可能存在的一些bug
似乎现在如果p太小或者$\alpha$太大的话,在迭代过程中可能出现概率为0的情况,因此如果库内无法正常选点触发异常,将输出此时这个节点上的总路径和