在上一篇文章中我曾经提到有一种较好的替代算法,A*算法来处理存在障碍物的情况下对路径的寻找
不过这种算法存在一个限制条件,就是其必须在网格内执行,而不是矢量(这看起来很正常,因为矢量的算法可以说几乎找不到)
同时由于这种算法的性质,其运算过程是难以矢量化的,所以直接拿python去跑会变得非常让人难以接受,因此我们必须拿C++来实现这个功能
具体而言,我们可以将这个问题转化为:网格化->A*寻路->矢量化三步进行
网格化
在进行网格化的过程中,我是首先制作了一个Mesh类,这个类中会储存已知起点和终点以及密度的网格.然后其中有一个方法,可以将现实坐标转化为网格坐标
之后,这个类提供一个接口,可以将首尾不相连的多边形转换为网格,其原理就是先转换首末端点,然后用Bresenham算法对直线进行绘制(这种方法避免浮点运算,效率较高)
这样就实现了对于坐标的网格化.
==索引问题==
由于在C中,数组的索引形式与
Eigen(一个C++扩展,支持线性代数运算,可以参考这个网页)相同,都是先行后列的索引因此我们会看到像
a[y][x]或是a(y,x)这样的索引在编写接口的过程中,需要多加小心
现在看好像并没有什么很显著的问题
==网格化的优化==
这种网格化提供了网格”生长”的可能性,例如在实际的操作中,我们知道机器必然不能精确的沿着边缘走,但是根据这一算法得到的结果,很多就是沿着边缘进行的
这个时候如果我们已经进行了网格化,就可以实现较为容易的计算机图形学中的膨胀操作
这里也许可以参考这篇文章
==向下舍入问题==
我们的计算是向下舍入的,即$a_x=(x-x_{beg})/\Delta x$一式向下舍入,那么我们在将网格倒推时,就需要加上0.5,减小误差
A*搜索
接下来就是我们讨论的A*搜索部分,实际上这一部分的内容网上都有,我就在这里给大家大略复述一下流程
创建一个
open_set和一个close_set从起点开始,将设定一个代价值(这个后面会讨论),然后将起点添加进
open_set中开始循环,直到达到终点:
- 取出
open_set中代价值最低的点,并将其加到close_set中 - 在这个点周围寻找满足条件(可达且未经过的点),并将这些点加到
open_set中
- 取出
如果达到终点,则回溯找到来时的路径,并返回
如果没有找到终点,那么终点不可达(有错误)
==关于代价函数==
我目前是使用曼哈顿距离作为代价函数进行计算实际上用欧几里得距离什么的也可以(但是计算效率会下降)
但是使用的代价函数必须满足一个条件:一个点的代价必须是唯一的(可以不同点有相同代价)
这与我们在算法中采用的
set有关,如果出现一个点有不同代价,那么比较函数将无法抵达红黑树树叶,然后就会出错必须满足传递原则:若a>b,b>c则a>c
==对于优化==
上面描述的是一般的代价函数,但是我们这里比较特殊,在进行计算前,我们需要对所有点进行初始化,此时一个起点对应的就不仅仅是一个终点了,也许可以极大的提高运算效率
反网格化
这里就相当于是网格化的逆过程,我也不必过多解释,但是要注意最后为了减小误差,需要加上半个步长
效果
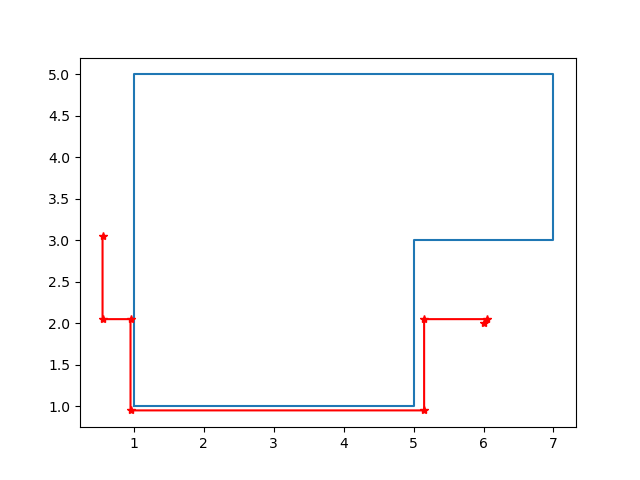
下面是我用python调取C++库采用曼哈顿距离作为代价函数的运行结果,蓝色线为障碍物边界,红色线为规划得到的路径,其效果非常可观.