关注闭环系统的控制系统设计(下)

使用模型匹配法进行增益调整

所谓模型匹配法就是通过指定合适的标准模型$\mathcal{M}(s)$尽量的去模拟目标值到控制量的传递函数$\mathcal{G}_{yr}(s)$
标准模型往往采用二项式系数标准型和巴特沃斯标准型
例如,二阶系统的标准模型为:
$$\mathcal{M}(s)=\frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}$$
当我们将阻尼系数$\zeta$设为$\zeta=1$时,就是二项式系数标准型,设为$\zeta=\frac{1}{\sqrt{2}}$为巴特沃斯标准型
而无阻尼自然振荡频率$\omega_n$为决定快速性的参数,值越大控制系统启动上升越快

而对于三阶系统,其标准模型为
$$\mathcal{M}(s)=\frac{\omega_n^3}{s^3+\alpha_2\omega_ns^2+\alpha_1\omega_n^2s+\omega_n^3}$$
当$(\alpha_1,\alpha_2)=(3,3)$时这个模型为二项式系数标准型,当$(\alpha_1,\alpha_2)=(2,2)$时这个模型为巴特沃斯标准型
此外,还有ITAE最小标准型,其可以使误差绝对值的时间加权积分最小,即
$$\int_0^t\tau|e(\tau)|\mathrm{d}\tau$$
值最小,可以将$(\alpha_1,\alpha_2)=(2.15,1.75)$

下面展示了各种标准模型效果

#准备工作
import matplotlib.pyplot as plt
import numpy as np
import control as ct 
from control.matlab import *
plt.rcParams['font.sans-serif'] = ['Simhei']  #显示中文
plt.rcParams['axes.unicode_minus'] = False    #显示负号
def line_generator():
    linestyle=["-","--","-.",":"]
    lineid=0
    while True:
        yield linestyle[lineid] #* 这个yield用法很有趣,可以学习一下
        lineid=(lineid+1)%len(linestyle)
def plot_set(fig_ax,*args):
    fig_ax.set_xlabel(args[0])
    fig_ax.set_ylabel(args[1])
    fig_ax.grid(ls=':')
    if len(args)==3:
        fig_ax.legend(loc=args[2])
def bodeplot_set(fig_ax,*args):
    fig_ax[0].grid(which='both',ls=':')
    fig_ax[0].set_ylabel('Gain [dB]')
    fig_ax[1].grid(which='both',ls=':')
    fig_ax[1].set_xlabel('$\omega$ [rad/s]')
    fig_ax[1].set_ylabel('Phase [deg]')
    if len(args)>0:
        fig_ax[1].legend(loc=args[0])
    if len(args)>1:
        fig_ax[0].legend(loc=args[1])

fig,axs=plt.subplots(1,2)
ls=line_generator()
omega=10
zetas=[1,1/np.sqrt(2)]
labels=["二项式系数标准型","巴特沃斯标准型"]
for zeta,label in zip(zetas,labels):
    p=tf([0,omega**2],[1,2*zeta*omega,omega**2])
    y,t=step(p,np.arange(0,2,0.01))
    axs[0].plot(t,y,next(ls),label=label)
plot_set(axs[0],"t","y","best")

alphas=[(3,3),(2,2),(2.15,1.75)]
labels=["二项式系数标准型","巴特沃斯标准型","ITAE最小标准型"]
for alpha,label in zip(alphas,labels):
    p=tf([0,omega**3],[1,alpha[0]*omega,alpha[1]*omega**2,omega**3])
    y,t=step(p,np.arange(0,2,0.01))
    axs[1].plot(t,y,next(ls),label=label)
plot_set(axs[1],'t','y','best')

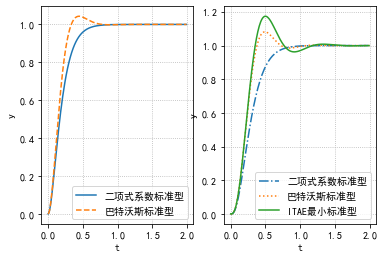
而模型匹配法是通过求取从$r$至$y$的传递函数,并且计算$\frac{1}{\mathcal{G}_{yr}(s)}$和$\frac{1}{\mathcal{M}(s)}$的麦克劳林展开式(即在$s=0$时的泰勒展开)按照顺序使其一致

简单而言就是在前面几阶近似下保持相同(可以假设$s$比较大)
例如机械臂模型,我们就可以有以下形式
$$\mathcal{G}_{yr}(s)=\frac{k_Ps+k_I}{Js^3+(\mu+k_D)s^2+(Mgl+k_P)s+k_I}$$
,我们可以利用Sympy库对于其进行展开

import sympy as sp
s=sp.Symbol('s')
kp,kd,ki=sp.symbols('k_p k_d k_i')
mgl,mu,j=sp.symbols('mgl mu j')
# sp.init_printing()
g=(kp*s+ki)/(j*s**3+(mu+kd)*s**2+(mgl+kp)*s+ki)
sp.series(1/g,s,0,4)

$\displaystyle \frac{mgl s}{k_{i}} + 1 + s^{2} \left(\frac{k_{d}}{k_{i}} + \frac{\mu}{k_{i}} - \frac{k_{p} mgl}{k_{i}^{2}}\right) + s^{3} \left(\frac{j}{k_{i}} - \frac{k_{d} k_{p}}{k_{i}^{2}} - \frac{k_{p} \mu}{k_{i}^{2}} + \frac{k_{p}^{2} mgl}{k_{i}^{3}}\right) + O\left(s^{4}\right)$

我们可以得到以上结果,与此同时,我们也可以展开$\frac{1}{\mathcal{M}(s)}$的方式得到另外一部分的结果

s=sp.Symbol('s')
omega,zeta=sp.symbols('omega zeta')
m=omega**2/(s**2+2*zeta*omega*s+omega**2)
sp.series(1/g,m,0,4)

$\displaystyle \frac{j s^{3} + k_{i} + s^{2} \left(k_{d} + \mu\right) + s \left(k_{p} + mgl\right)}{k_{i} + k_{p} s}$

联立两式,我们就可以得到$k_P,k_I,k_D$,在我们这种二阶滞后系统的情况下,可以实现$\frac{1}{\mathcal{G}_{yr}(s)}$和$\frac{1}{\mathcal{M}(s)}$完全一致

这是因为两者阶数恰好相同所以可以完全一致,但是在实际情况下只能大致相同

状态反馈控制

我们前面研究的是关于传递函数的模型,现在我们来研究状态空间模型$\dot{x}=Ax+Bu$所描述的系统
状态空间模型除了输入和输出,还存在有状态,我们可以假定可以通过传感器等观测到这些信息,具体而言,我们考虑如下的状态反馈控制:
$$u=Fx$$
通过利用状态$x$的信息,来确定控制输入$u$,此处$F$称为状态反馈增益
我们可以将状态反馈控制看作为一种PD控制,例如对于我们之前讨论的手推车系统,我们可以将手推车的位置$z$和速度$\dot{z}$当作状态,那么上式就可以被写作:
$$u=Fx=f_1z+f_2\dot{z}$$
其中$f_1$为比例增益,$f_2$为微分增益
而在状态反馈控制中最具代表性的设计方法有两种,分别为极点控制法和最优调节器

极点配置法

将状态反馈控制$u=Fx$施加于系统$\dot{x}=Ax+Bu$上之后,闭环系统可以写作如下形式:
$$\dot{x}=(A+BF)x$$
倘使和矩阵的所有极点的实部均为负数,那么系统是稳定的

这里提醒一下,和矩阵的所有特征值实部均为负数(因为是在e指数上)

做法是这样的:

找到我们所需的特征值
寻找$F$,使$A+BF$能够满足我们的需要利用acker函数自带的阿克曼极点配置算法

A='0 1;-4 5'
B='0; 1'
C='1 0;0 1'
D='0;0'
P=ss(A,B,C,D)

pole=[-1,-1] #*指定极点
F=-acker(P.A,P.B,pole)

这里有负号的原因是在于acker返回的是使$A-BF$的特征值作为指定极点的$F$
我们可以验证一下特征值是否正确

1	np.linalg.eigvals(P.A+P.B*F)

array([-1.+6.68896751e-09j, -1.-6.68896751e-09j])

几乎就是1(前面的应该是float的误差),那么我们来看一下闭环控制系统的行为

acl=P.A+P.B*F
pfb=ss(acl,P.B,P.C,P.D)
td=np.arange(0,5,0.01)
x0=[-0.3,0.4]
x,t=initial(pfb,td,x0)
fig,ax=plt.subplots()
ax.plot(t,x[:,0],label="$x_1$")
ax.plot(t,x[:,1],ls="-.",label="$x_2$")
plot_set(ax,"t","x","best")

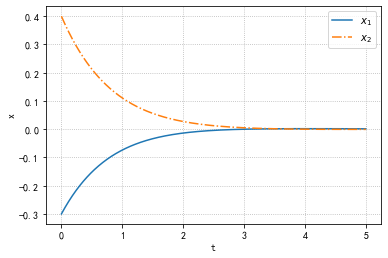
对于特征值的选定

最优调节器

我们既然已经知道了极点配置法如何工作,那么我们需要评估其结果,主要有两点特征:

特征值实部负值越大响应越快,但是反馈增益$F$也会变大导致输入非常大
状态变量可能会出现涨幅较大的变量
为了解决这个问题,我们可以设定某个评价指标,同时求取状态反馈增益令评价指标最小化

对于$Q=Q^T>0,R=R^T>0$,有以下的评价函数
$$J=\int^\infin_0(x^T(t)Qx(t)+u^T(t)Ru(t))dt$$
使得这个函数最小化的控制器形式为$u=F_{opt}x$,其中$F_{opt}$的值为
$$F=-R^{-1}B^TP$$
其中$P=P^T>0$,是满足下述方程的唯一正定二次型
$$A^TP+PA+PBR^{-1}B^TP+Q=0$$
那么$J$的最小值为$x(0)^TPx(0)$
(仔细看评价函数,两个二次型)

像这样通过评价函数最优化得到的状态反馈控制为最优调节器
另外,我们通常设定$Q$为对角阵(标准型),其中$Q$的对角元往往用来表示哪个先收敛
相应的,在$u$恒定的条件下,$R$作为标量越大,就可以得到不会让输入过大的$F$
而在python中,我们可以使用lqr来设计最优调节器

Q=[[100,0],[0,1]] #*使用这个Q表示我们要让状态第一个变量速度大
R=100

F,X,E=lqr(P.A,P.B,Q,R)#*F为得到的反馈增益(要加一个负号),X为里卡提方程的解,E则为这个闭环系统的极点
F=-F
print("反馈增益".center(50,'-'))
print(F)#使用-(1/R)*B.T*X也能有相似的效果
print("闭环极点".center(50,'-'))
print(E)
acl=P.A+P.B*F
pfb=ss(acl,P.B,P.C,P.D)
td=np.arange(0,5,0.01)
x0=[-0.3,0.4]
x,t=initial(pfb,td,x0)
fig,ax=plt.subplots()
ax.plot(t,x[:,0],label="$x_1$")
ax.plot(t,x[:,1],ls="-.",label="$x_2$")
plot_set(ax,"t","x","best")

-----------------------反馈增益-----------------------
[[ -0.12310563 -10.02555582]]
-----------------------闭环极点-----------------------
[-1.03259306 -3.99296276]

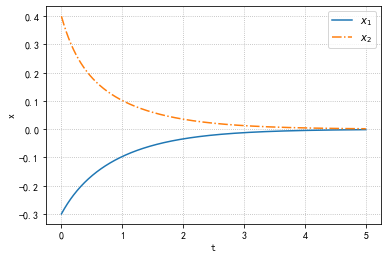
使用care也可以得到相似的结果,在此不再介绍

还有,我想当怀疑这个状态空间就是所谓的相空间,太像了(但是维度又不止二维)

同时,前面使用配置极点法时,要求任意状态$x$开始,要能够达到相空间的任何地方,可以使用ctrb求可控性矩阵

闭环系统规格

	随动系统	恒值调节系统
阻尼系数	0.6~0.8	0.2~0.5
超调量	0~0.25	0~0.25
峰值增益	1.1~1.5	1.1~1.5