关注闭环系统的控制系统设计(上)

对于一个被控制对象$\mathcal{P}$,我们需要搭建一个反馈控制系统,如图所示:

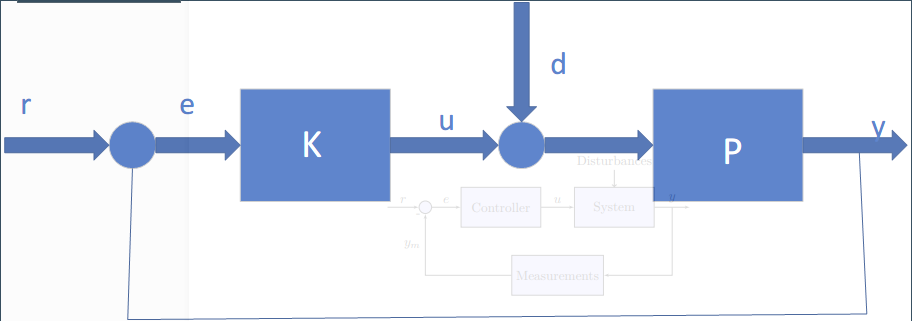
其中$\mathcal{K}$为控制器,$r$为目标值,$u$为控制输入,$d$为扰动,$y$为输出,$e$为误差,下面来分别介绍稳定性,时域特性以及频域响应特性

设计规格

稳定性

对于闭环系统,外部输入有$r$和$d$,输出包含了被控对象的输出$y$和控制器的输出$u$,因此闭环系统要同时考虑从$r,d$到$u,y$总共四个稳定性
通过相关的数学计算,若其特征多项式$\phi(s)=D_P(s)D_K(s)+N_P(s)N_K(s)$(其中$\mathcal{P}(s)=\frac{N_P(s)}{D_P(s)}$)的根是稳定的,系统内部就是稳定的

这一个过程利用传递函数法不难推导

时域响应特性

从发生阶跃到逐渐稳定的过程由许多部分组成,在响应中振荡的部分被称作瞬态特性,而当经过足够长时间后振荡收敛的部分则被称为稳态特性

而对瞬态特性进行定量评价的指标有:上升时间(从10%-90%),调整时间(稳定在$\pm$%5),峰值时间,过冲,对于稳态响应进行定量评价的则为稳态误差,其描述目标值和稳定值之间的差

频域响应特性

描述瞬态特性的指标有通频带$\omega_{bw}$(幅值下降约3dB的频率)和峰值增益$M_p$,往往在峰值增益处叫作协助峰值

闭环系统的设计规格

根据我们之前所讨论的,在控制系统的设计中闭环系统应当满足以下条件:

稳定性
快速性(通频带较大)
阻尼特性(峰值增益较小)
稳态特性(直流增益为1)

PID控制

PID分为三个部分构成:

P:比例(Partial),现在的信息,实时误差
I:积分(Integral),过去的信息
D:微分(Derivative),未来的信息
只用P,可以让系统稳定,但是无法移动到目标位置,使用PI,可以让系统达到目标,但是会振荡

使用公式来表述PID控制,可以写为:
$$u(t)=k_pe(t)+k_1\int^t_0 e(t_s)\mathbf{d}t_s+k_D\dot{e}(t)$$
而对其进行拉普拉斯变换则得到:
$$u(s)=\frac{k_Ds^2+k_Ps+k_1}{s}e(s)$$

#准备工作
import matplotlib.pyplot as plt
import numpy as np
import control as ct 
from control.matlab import *
def line_generator():
    linestyle=["-","--","-.",":"]
    lineid=0
    while True:
        yield linestyle[lineid] #* 这个yield用法很有趣,可以学习一下
        lineid=(lineid+1)%len(linestyle)
def plot_set(fig_ax,*args):
    fig_ax.set_xlabel(args[0])
    fig_ax.set_ylabel(args[1])
    fig_ax.grid(ls=':')
    if len(args)==3:
        fig_ax.legend(loc=args[2])
def bodeplot_set(fig_ax,*args):
    fig_ax[0].grid(which='both',ls=':')
    fig_ax[0].set_ylabel('Gain [dB]')
    fig_ax[1].grid(which='both',ls=':')
    fig_ax[1].set_xlabel('$\omega$ [rad/s]')
    fig_ax[1].set_ylabel('Phase [deg]')
    if len(args)>0:
        fig_ax[1].legend(loc=args[0])
    if len(args)>1:
        fig_ax[0].legend(loc=args[1])

P控制性能

如下图所示的P控制系统是通过误差来按照比例计算控制输入的

下面以机械臂(二姐滞后系统)为例,看看P控制效果

下面这段代码描述了模型

1
2
3

g,l,M,mu,J=9.81,0.2,0.5,1.5e-2,1e-2
P=tf([0,1],[J,mu,M*g*l])
ref=30#目标位置

我们来试试不同的比例增益阶跃响应会是如何

kp=(0.5,1,2)
ls=line_generator()
fig,ax=plt.subplots()
for i in range(3):
    K=tf([0,kp[i]],[0,1])#P控制
    gyr=feedback(P*K,1)#形成反馈系统
    y,t=step(gyr,np.arange(0,2,0.01))#这里与参考之间是归一化
    pltargs={'ls':next(ls),'label':'$k_P$='+str(kp[i])}
    ax.plot(t,y*ref,**pltargs)
ax.axhline(ref,color='k',linewidth=0.5)
plot_set(ax,'t','y','best')

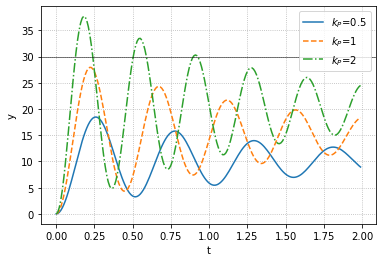
可以注意到,只使用P控制无法实现达到目标位置,但是$k$越大,离目标位置越近

这里有一个理解上的问题,这里的输入实际上是预期值,结果P控制后才转化为像力矩一样的东西

我们接下来看看这个系统的伯德图

ls=line_generator()
fig,ax=plt.subplots(2,1)
for i in range((len(kp))):
    k=tf([0,kp[i]],[0,1])
    gyr=feedback(P*k,1)
    gain,phase,w=bode(gyr,logspace(-1,2),plot=False)
    pltargs={'ls':next(ls),'label':'$k_P$='+str(kp[i])}
    ax[0].semilogx(w,20*np.log10(gain),**pltargs)
    ax[1].semilogx(w,phase*180/np.pi,**pltargs)
bodeplot_set(ax,'best')

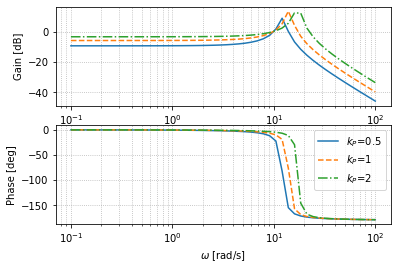
可以注意到,随着$k_P$的增加,通频带在增加,但系统也会更加振荡

PD控制

刚才我们看到了,随着$k_P$的逐渐增大,振荡也会变大,可以通过添加D控制来控制振荡.
PD控制如下图所示,为$\mathcal{K}(s)=k_Ds+k_P$

我们可以用以下代码对PD控制进行模拟

kp=2
kd=(0,0.1,0.2)
ls=line_generator()
fig,ax=plt.subplots()
for i in range(3):
    k=tf([kd[i],kp],[0,1])#PD控制
    gyr=feedback(P*k,1)
    y,t=step(gyr,np.arange(0,2,0.01))
    pltargs={'ls':next(ls),'label':'$k_D$='+str(kd[i])}
    ax.plot(t,y*ref,**pltargs)
ax.axhline(ref,color='k',linewidth=0.5)
plot_set(ax,'t','y','best')

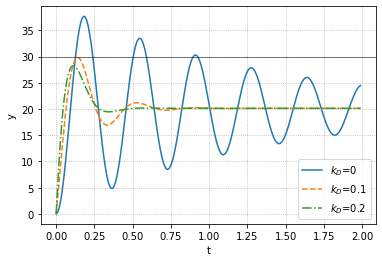
我们可以注意到,在有D控制的情况下,振荡得到了有效的抑制,但是稳态误差不为0
我们接下来来研究一下闭环系统的伯德图

ls=line_generator()
fig,ax=plt.subplots(2,1)
for i in range(3):
    k=tf([kd[i],kp],[0,1])
    gyr=feedback(P*k,1)
    gain,phase,w=bode(gyr,logspace(-1,2),plot=False)
    pltargs={'ls':next(ls),'label':'$k_D$='+str(kd[i])}
    ax[0].semilogx(w,20*np.log10(gain),**pltargs)
    ax[1].semilogx(w,phase*180/np.pi,**pltargs)
bodeplot_set(ax,'best')

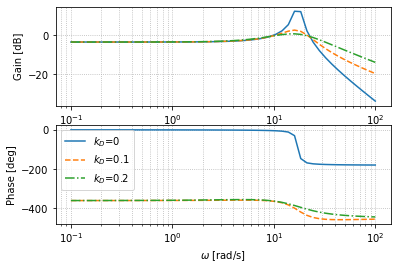
这里$k_D$等于0的相位有点问题,但是我就懒得调了,可以看出,随着$k_D$的增大,通频带会逐渐增大,且过冲会减小,但是稳态条件下并没有改善

PD控制的可实现性
我们需要注意到PD控制的传递函数是非真分的,即控制过程中会用到系统未来的信息,因此我们需要使用不完全微分
$$\frac{s}{1+T_{lp}s}$$
这是将低通滤波(一阶滞后系统)叠加到微分后的结果,是真分的函数(即添加一个对输出求导的函数)

PID控制

最后,我们为了改善稳态的特性,我们可以添加I控制可以让稳态误差为0,同时,我们也可以注意到,随着$k_I$增大,振荡也会增强

kp=2
kd=0.1
ki=(0,5,10)
ls=line_generator()
fig,ax=plt.subplots()
for i in range(3):
    k=tf([kd,kp,ki[i]],[1,0])
    gyr=feedback(P*k,1)
    y,t=step(gyr,np.arange(0,2,0.01))
    pltargs={'ls':next(ls),'label':'$k_I$='+str(ki[i])}
    ax.plot(t,y*ref,**pltargs)
ax.axhline(ref,color='k')
plot_set(ax,'t','y','best')

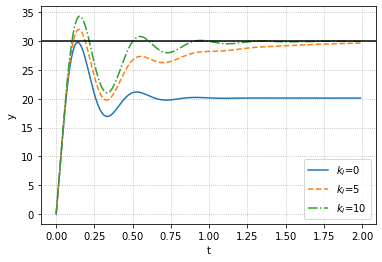
接下来,我们来观察一下PID控制的伯德图

ls=line_generator()
fig,ax=plt.subplots(2,1)
for i in range(3):
    k=tf([kd,kp,ki[i]],[1,0])
    gyr=feedback(P*k,1)
    gain,phase,w=bode(gyr,logspace(-1,2),plot=False)
    pltargs={'ls':next(ls),'label':'$k_I$='+str(ki[i])}
    ax[0].semilogx(w,20*np.log10(gain),**pltargs)
    ax[1].semilogx(w,phase*180/np.pi,**pltargs)
bodeplot_set(ax,'best')

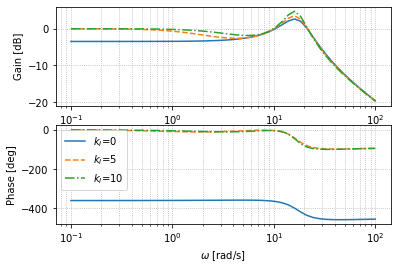
我们可以注意到,随着$k_I$的增大,振荡会增大,但是其他性质近似能够保持不变

我们还可以来研究一下抗干扰性
因为可能会从d出现输入(扰动),下面展示了当d为阶跃输入时的系统整体的变化
这些扰动在机械系统中往往是一些摩擦等因素

ls=line_generator()
fig,ax=plt.subplots()
for i in range(3):
    k=tf([kd,kp,ki[i]],[1,0])
    gyd=feedback(P,k)#注意这里反馈环的变化
    y,t=step(gyd,np.arange(0,2,0.01))
    pltargs={'ls':next(ls),'label':'$k_I$='+str(ki[i])}
    ax.plot(t,y,**pltargs)
plot_set(ax,'t','y','best')

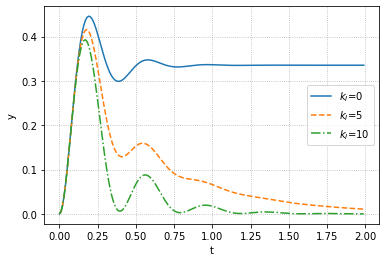
可以注意到,虽然有振荡,但是I控制最终总是能够拉回

PID数学形式
闭环系统:
$$\frac{k_Ds^2+k_Ps+k_I}{Js^3+(\mu +k_D)s^2+(mgl+k_P)s+k_I}$$
当频率为0(稳态时),闭环系统为1
扰动:
$$\frac{s}{Js^3+(\mu +k_D)s^2+(mgl+k_P)s+k_I}$$
当频率为0(稳态扰动时),扰动影响为0

二自由度控制

但是在实际的使用过程中,我们往往使用的是PID控制的改良版本,我们下面介绍改良版的PID控制以及其与二自由度控制之间的关系.
在PID控制中如果目标值以阶跃状变化时控制输入($u(t)$)就会出现微分器中包含的冲激成分(虽然这个值不会像理论计算那样是无穷大,但是也会非常大).因此我们有时会将微分器移动到输出(这样不会直接输入)的PI-D控制,可以用下式表示
$$u(s)=k_Pe(s)+\frac{k_I}{s}e(s)-k_Dsy(s)$$
其控制框图如图所示:
而对于P控制,输入中也存在有阶跃状的信号,而为了解决这个问题,我们也可以将P也放到输出端,那么可以用下式表述:
$$u(s)=-k_Py(s)+\frac{k_I}{s}e(s)-k_Dsy(s)$$
PI-D控制和P-ID控制就是在反馈控制基础上叠加了顺馈控制的二自由度控制,下面对其加以介绍:
对于PI-D控制,我们可以通过计算其输入$u(s)$为:
$$u(s)=\frac{k_Ds^2+k_Ps+K_I}{s}\left(\frac{k_Ps+k_I}{k_Ds^2+k_Ps+k_I}r(s)-y(s)\right)=\mathcal{K}_1(s)(\mathcal{K}_2(s)r(s)-y(s))$$
可以看作是两个控制器$\mathcal{K}_1$就是普通的PID控制,而$\mathcal{K}_2$则为一个滤波器,可以将输入信号变得平滑
相似的,对于P-ID控制,形式与前相同,只是$\mathcal{K}_2$变成了
$$\mathcal{K}_2(s)=\frac{k_I}{k_Ds^2+k_Ps+k_I}$$
我们可以看看PID控制与PI-D控制以及I-PD控制之间区别

kp,ki,kd=2,5,0.1
pcontrol=tf([0,kp],[0,1])
icontrol=tf([0,ki],[1,0])
dcontrol=tf([kd,0],[0,1])
#首先看看PID控制
pid=parallel(pcontrol,icontrol,dcontrol)
fb=feedback(pid*P,1)
pidout,t=step(fb,np.arange(0,3,0.01))
fig,ax=plt.subplots()
ax.plot(t,pidout,'r-',label="PID")
#接下来是PI_D控制
pi=parallel(pcontrol,icontrol)
Pd=feedback(P,dcontrol)
gyd=feedback(pi*Pd,1)
pi_dout,t=step(gyd,np.arange(0,3,0.01))
ax.plot(t,pi_dout,'g-',label="PI-D")
#最后是P_ID控制
Ppd=feedback(P,parallel(pcontrol,dcontrol))
gyd=feedback(icontrol*Ppd,1)
p_idout,t=step(gyd,np.arange(0,3,0.01))
ax.plot(t,p_idout,'b-',label="P-ID")

plot_set(ax,'t','y','best')
plt.show()

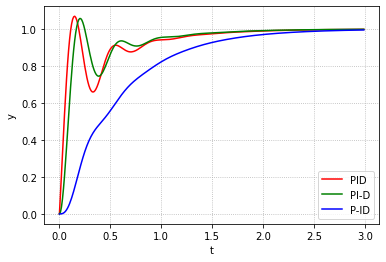
可以注意到,使用PI-D振荡会略小,而使用P-ID振荡则几乎消失(这样可以避免u输入过大)

使用临界比例度法进行增益调整

常见有两种调节PID增益的方法,它们分别是临界比例度法和阶跃响应法,这里我们主要是研究使用临界比例度法对PID增益的调整,这种方法好处在于无需知道被控对象的模型,但是也有着相应的缺点:必须重复实验并且将机器运行在极其不稳定状态
在使用临界比例度法时,首先搭建一个P控制,然后逐渐增大比例增益$k_P$,此时振荡也会逐渐增大
此时我们可以来调查比例增益$k_{P0}$和持续振荡的周期$T_0$,在实际的系统中,由于存在有微小的延迟时间,因此会产生持续振荡

得到了这些信息,我们就可以根据下表来确定比例增益$k_P$,积分时间常数$T_I$和微分时间常数$T_D$,对于PID控制,有:
$$u(t)=k_P\left(e(t)+\frac{1}{T_I}\int e(t)dt+T_D\frac{d}{dt}e(t)\right)$$
则有$k_I=\frac{k_P}{T_I}$,$k_D=k_PT_D$

临界比例度法	比例增益$k_P$	积分时间常数$T_I$	微分时间常数$T_D$
P控制	0.5 $k_{P0}$
PI控制	0.45 $k_{P0}$	0.83 $T_0$
PID控制	0.6 $k_{P0}$	0.5 $T_0$	0.125 $T_0$
无过冲控制	0.2 $k_{P0}$	0.5 $T_0$	0.33 $T_0$

下面我们假设处理的是作为被控对象的二阶滞后系统中存在有微小的延迟时间

延迟系统可以表示为$e^{-hs}$这样的无穷维系统,可以近似为有理函数,下面使用一阶帕德近似,延迟时间设定为0.005

1 2	numd,dend=pade(0.005,1) Pdelay=P*tf(numd,dend)

我们按照要求将比例增益大概调节到2.9并且施加P控制,那么就会产生下图所示的振荡

fig,ax=plt.subplots()
kp0=2.9
K=tf([0,kp0],[0,1])
gyr=feedback(Pdelay*K,1)
y,t=step(gyr,np.arange(0,2,0.01))

ax.plot(t,y)
ax.axhline(1)
plot_set(ax,'t','y')

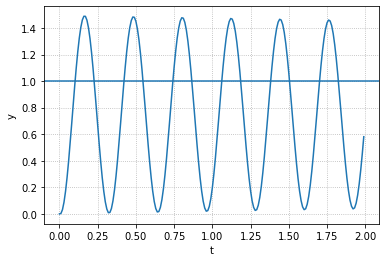
可以注意到,系统已经产生了显著的振荡,我们可以读出持续振荡的周期约为0.3s,那么我们就可以用这个系统来实现PID控制

kp=[0,0]
ki=[0,0]
kd=[0,0]
t0=0.3
kp[0]=0.6*kp0
ki[0]=kp[0]/(0.5*t0)
kd[0]=kp[0]*(0.125*t0)
K=tf([kd[0],kp[0],ki[0]],[1,0])
fig,ax=plt.subplots()
gyr=feedback(K*Pdelay,1)
y,t=step(gyr,np.arange(0,2,0.01))
ax.plot(t,y)
plot_set(ax,'t','y')

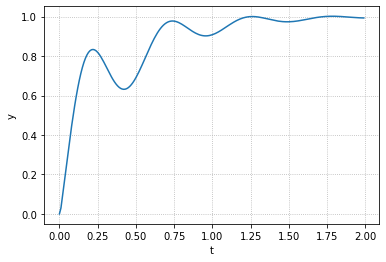
可以看到,实现了较好的控制,我们还可以避免过冲,可以看以下代码

kp=[0,0]
ki=[0,0]
kd=[0,0]
t0=0.3
kp[0]=0.2*kp0
ki[0]=kp[0]/(0.5*t0)
kd[0]=kp[0]*(0.33*t0)
K=tf([kd[0],kp[0],ki[0]],[1,0])
fig,ax=plt.subplots()
gyr=feedback(K*Pdelay,1)
y,t=step(gyr,np.arange(0,2,0.01))
ax.plot(t,y)
plot_set(ax,'t','y')