经过数日的鏖战,我算是把一个路径规划程序给写完了,然而,这其中隐藏着不少的问题,以至于虽然这个程序理论上能够给出正确答案,但是实际上由于某些原因完全无法使用,下面我将这个记录下来,以供参考
程序目的
因为我们研究的磁场中存在物体,因此不能简单的整个空间到处跑,而是要根据物体的位置,进行避障,避完障之后还要选择一个尽量好的路径
虽然说后者是一个典型的旅行商问题,显然是不可能在多项式时间以内完成的,但是我们这里不是算法题,并且实际计算的点并不多,因此并不是最为复杂的
但是前面一个问题就要复杂的多,因为我没有学过计算机图形学,只能自己猜应该怎么做,之后可以查一些别的资料(好像在这一部分可以用蚁群算法实现)
下面我就来介绍一下我的这个程序是如何工作的
程序整体框架
下图展示了这个程序的整体框架
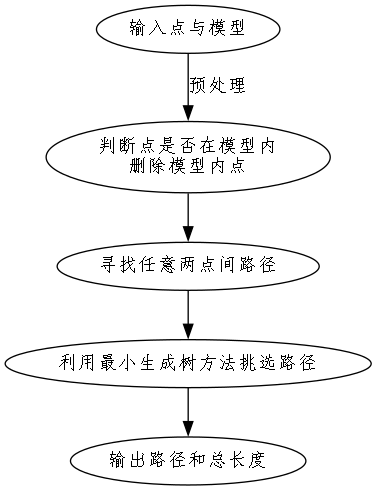
算法内容
这些算法可以参考以下内容
我们主要要讲的是中间寻找任意两点间路径这一部分实现
寻找任意两点间路径
寻找任意两点间的路径算法如下
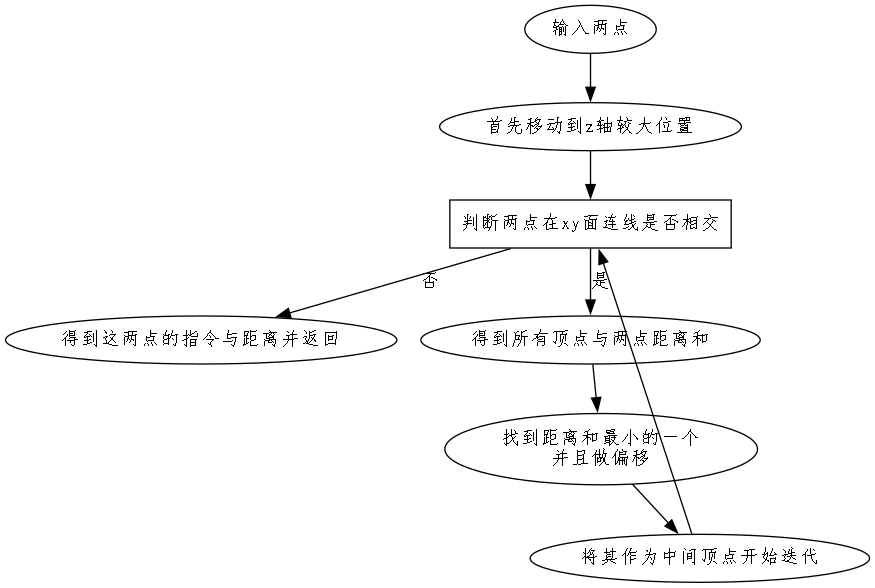
这中间有一个找顶点做偏移的步骤,理论上来说是可以贴边不偏移的,但是实际上你那么做的时候由于凹多边形,两个顶点都在边上时你难以判断这条线是不是在模型里面
也许我们可以在线上随机取点判断是否在模型中,但这未免太麻烦
于是我就用一个小的偏移,在顶点处两线交汇处的角平分线移动一小段距离作为新的顶点
这种方法偏移太大自然不行,但是偏移太小也会导致点判断错误,这与判断点是否在障碍物内算法有关
运行结果
我拿了一个非常简单的模型进行了尝试,结果它硬生生跑了好久,最后扔给我这样一个结果

红色的是障碍物轮廓,蓝色的是规划的路径
确实其给了我一个可行答案,但是这个答案并不好,而且获得答案的代价不可接受
我认为主要原因来自于避障规划使用贪心算法,会给出并不一定好的结果,但是并不能用上贪心算法的高效
无疑这个问题还需要查阅更多的资料