Songyuli's blog
0%

处理3D模型

Posted on In Disqus:

为了实现通过用户给的3D模型实现避障功能的路径规划,我们采取首先对模型进行切片,然后再通过修改路径长度和两点之间路径获取的函数完成

对于meshcut库的使用

可以实现3D建模处理的库有很多,但如果仅仅是想要一个切面就将vtk搬出来未免就有一点大材小用了,通过寻找,我找到了一个meshcut库,其可以将stl文件和定义的平面求得交线.

meshcut库的开发主页

下面是使用meshcut库实现对一个3D模型切割的效果图

42

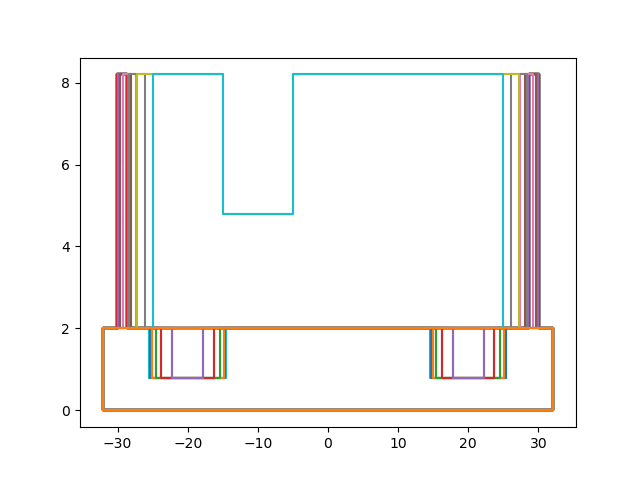
而其所使用的源码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import stl
import matplotlib.pyplot as plt
import numpy as np
import meshcut

def create_mesh(m:stl.mesh.Mesh):#从stl文件中创建mesh
    # Flatten our vert array to Nx3 and generate corresponding faces array
    verts = m.vectors.reshape(-1, 3)
    faces = np.arange(len(verts)).reshape(-1, 3)

    verts, faces = meshcut.merge_close_vertices(verts, faces)
    return meshcut.TriangleMesh(verts,faces)

if __name__=="__main__":
    m=stl.mesh.Mesh.from_file("up.stl")
    mesh=create_mesh(m)

    i=1
    z=1#z坐标
    while(i!=0):#在没有交点是会报错,程序自动终止
        plane_origin=np.array([0,0,z])
        plane_n=np.array([0,0,1])
        plane=meshcut.Plane(plane_origin,plane_n)#创建平面

        p=meshcut.cross_section_mesh(mesh,plane)#求解相交部分多边形
        x=p[0][:,0]
        x=np.hstack([x,np.array(x[0])])
        y=p[0][:,1]
        y=np.hstack([y,np.array(y[0])])
        plt.plot(x,y)
        plt.savefig("{}.png".format(z))
        z=z+1

判断一条线是否与多边形相交

算法

接下来我们来讨论一下关于碰撞检测这一部分的内容.

多边形是由有限个点首尾相连而成的,那么假如一条线段与多边形相交,那么其必然与多边形的至少一条边相交.因此问题就转化为判断一条线段是否与一个线段集中线段相交.

而对于判断两线段是否相交的方法,记第一条线段两点为$A_1,A_2$,第二条线段两点为$B_1,B_2$,如果从线段一指向线段二某点(通常使用某个端点)的两个矢量与线段二的叉乘异号,表明$A_1,A_2$分别位于第二条线段两侧.同理,可以判断$B_1,B_2$是否位于第一条线段两侧.如果两个条件同时满足,那么就可以说明线段相交.

这一手段参考资料

特殊情况,判断点是否在多边形内,可以用相似的方法,通过过该点做一条射线,然后统计相交点数,如果相交点数为偶数,则点在多边形内,否则在多边形外

实现

在实现这个问题的同时,需要考虑到Python在处理大量的for循环时效率非常低下,因此需要对操作进行向量化处理.

假定$A_x,A_y,B_x,B_y$为$n,n,m,m$维列向量,定义$C_{ij}$的值等于$A_{i}\times B_{j}$为行列式的值,根据线性代数相关知识,我们可以得到$C=A_xB^T_y-A_yB_x^T$

如此操作时需要注意对array进行reshape

下面展示了实现矢量集叉乘和判断线段集是否相交的代码

1
2
3
4
5
6
7
def calc_cross(a: np.array, b: np.array):
        # 计算两个二维向量集的叉乘
        ax = a[:, 0].reshape(-1, 1)
        ay = a[:, 1].reshape(-1, 1)
        bx = b[:, 0].reshape(1, -1)
        by = b[:, 1].reshape(1, -1)
        return np.dot(ax, by)-np.dot(ay, bx)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def check_crossing(lines1: np.array, lines2: np.array):
        begs1 = lines1[:, 0, :]
        begs2 = lines2[:, 0, :]
        ends1 = lines1[:, 1, :]
        ends2 = lines2[:, 1, :]
        l1 = ends1-begs1
        l2 = ends2-begs2

        # 检查线2是否分隔线1
        v1 = begs2-begs1
        v2 = begs2-ends1
        c1 = calc_cross(v1, l2)
        c2 = calc_cross(v2, l2)
        c = c1*c2  # 计算两矩阵各个元素相乘(比较同号异号)
        bca = c < 0  # 分割线1

        # 检查线1是否分隔线2
        v1 = begs1-begs2
        v2 = begs1-ends2
        c1 = calc_cross(v1, l1)
        c2 = calc_cross(v2, l1)
        c = c1*c2  # 计算两矩阵各个元素相乘(比较同号异号)
        bcb = c < 0  # 分割线2

        bc = np.all([bca, bcb], axis=0)  # 同时分割
        return bc  # 第i行第j列元素判断lines1的第i根线与lines2的第j根线是否相交

这个时候我意识到了一个问题:在实际的移动过程中,z轴的移动无法控制,因此需要在路径规划的过程中对z轴进行单独处理

因此:在每一次移动时,首先移动z轴,然后就可以理解为平面内运动